Can You (Not) Flip Your Lid?

Riddler Express

The other day I was playing around in my kitchen with a tall glass and a smaller disk, when, to my surprise, I was able to balance the disk neatly atop the rim of the glass:

First of all, try this at home!

Now suppose you have a disk of radius R and a glass with a circular rim of radius 2R. If you randomly place the disk so that its center lies within the glass’s rim, what is the probability that the disk will balance atop the glass? (Assume the distribution is uniformly spread across the circular area inside the rim.)

Solution

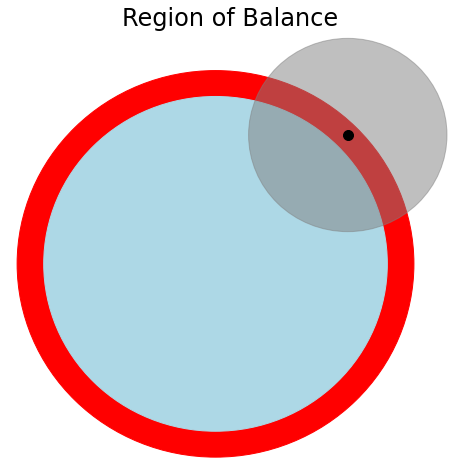
The center of the disk needs to be within the triangle defined by the two intersection points of the glass and the disk and the third point lying on the glass circumference, collinear with the center of the glass and disk.

In the diagram on the left below, if the disk is pushed any further inside, the chord will decrease, and the center of the disk will be in the exterior of the triangle.

In the diagram on the right below, if the disk is pushed any further outside, the center of the disk, currently coinciding with the third point of the triangle, will fall outside the circumference of the glass.

Note that on the left, the chord is the diameter. The distance of the center of the disk from the center of the glass is the height of an equilateral triangle with side $2R$, which is $R\sqrt{3}$.

On the right, the distance of the center of the disk from the center of the glass is $2R$.

The diagram below denotes the acceptable region for balance in red.

The probability that the disk will balance atop the glass is :

$$\dfrac{(2R)^2 - (R\sqrt{3})^2}{(2R)^2}$$

$$ = \dfrac{4R^2 - 3R^2}{4R^2} = \dfrac{1}{4}$$

Rohan Lewis

2020.12.21

Code can be found here.