Can You Cut The Cookies?

Riddler Classic

From Dean Ballard come trials and tribulations of troublesome triangles:

Three friends are baking holiday cookies together. They have a flat layer of cookie dough in the shape of an isosceles right triangle (shown below). They want to design a cookie cutter that will cut out three identical (i.e., congruent) cookies. The cookies should be as large as possible while staying within the triangle and without overlapping each other.

Had there been two friends or four friends, they would have been able to use all of the cookie dough. But with three friends, there will unfortunately be some cookie dough that goes to waste.

What is the greatest percentage of cookie dough that can be made up by the three identical cookies? When explaining your work, please be as detailed as you can about the arrangement of your cookies so I can verify your work!

Extra credit: Instead of a right isosceles triangle, the three friends now want to make identical cookies from a sphinx of cookie dough. Again, what is the greatest percentage of cookie dough that can go into the three identical cookies?

Solution

The following picture has the maximum cookie area by three identical shapes within the dough.

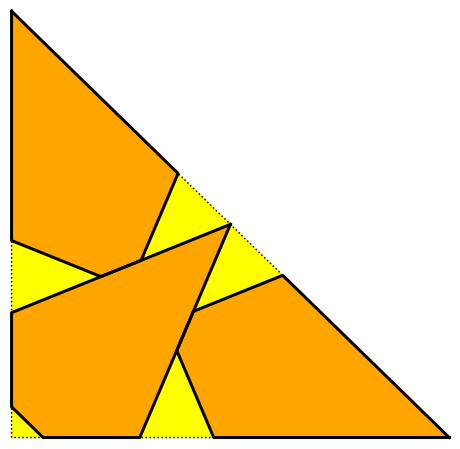
To find the area a close up is shown.

Set the original isosceles triangle dough as having legs $= 1$.
$$m = \dfrac{1}{2}\tan(22.5°) = \dfrac{1}{\sqrt{2}} -\dfrac{1}{2} \approx 0.2071$$
$$n = \dfrac{\frac{1}{2}}{\cos(22.5°)} = \dfrac{1}{2\cos(22.5°)} \approx 0.5412$$
The hypotenuse of the dough can be expressed as:
$$2n + 2p = \sqrt{2}$$
$$p = \dfrac{\sqrt{2} - 2n}{2} = \dfrac{1}{\sqrt{2}} - n \approx 0.1659$$
Using similar triangles and their respective hypotenuse and short leg:
$$\dfrac{q}{\frac{p}{2}} = \dfrac{n}{m}$$
$$q = \dfrac{np}{2m} = \dfrac{0.5412 \cdot 0.1659}{2 \cdot 0.2071} \approx 0.2168$$
Using the left side:
$$r = \frac{1}{2} - m - q = 0.5 - 0.2071 - 0.2168 \approx 0.0761$$
The area of the cookie can be found by subtracting the three right triangles from the $\frac{1}{2}$x$\frac{1}{2}$ square.

$$Area = \Big(\dfrac{1}{2}\Big)^2 - 2 \cdot \Big(\dfrac{m \cdot \frac{1}{2}}{2}\Big) - \dfrac{r^2}{2}$$
$$ = 0.25 - 0.1036 - 0.0029 \approx 0.1435$$

Answer

Three cookies out of the dough yields:
$$\dfrac{3 \cdot 0.1435}{0.5} \approx 86.1\%$$.

Update

I realized two days later there is a better answer. :(

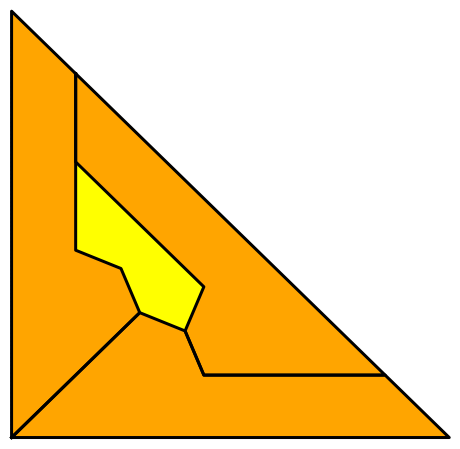
To find the area a close up is shown. The areas of both figures above are identical, although the shapes are made in slightly different ways.

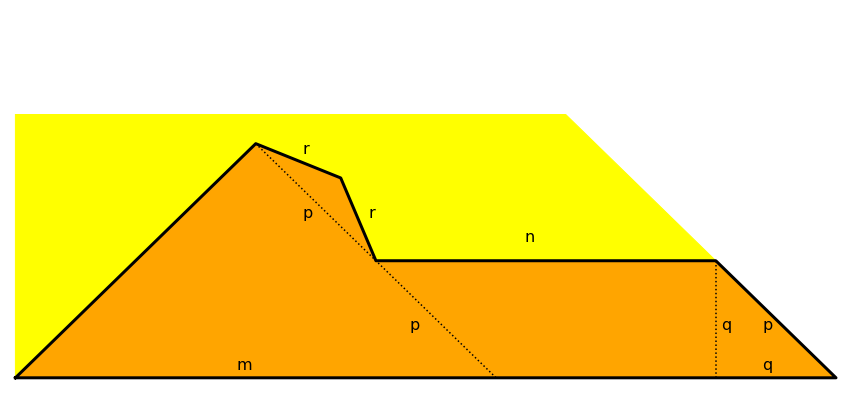
The leg of the dough is $1 = m + n$

$p$ can be determined from the hypotenuse of the dough:

$$(m + n) + 2p = \sqrt{2}$$

$$p = \dfrac{\sqrt{2} - 1}{2}$$

$q$ can be determined from isoceles right triangle on the far right: $$q = \dfrac{p}{\sqrt{2}} = \dfrac{\sqrt{2} - 1}{\sqrt{8}}= \dfrac{2 - \sqrt{2}}{4}$$

$m$ can be determined from isoceles right triangle on the left: $$m = 2p \cdot \sqrt{2} = 2 - \sqrt{2}$$

$n$ can be determined from the leg of the dough: $$n = 1 - m = \sqrt{2} - 1$$

Note $n = 2\cdot p$ from the cookie along the hypotenuse of the dough.

The small isosceles triangle in the center with $r$, $r$, and $p$ is $22.5°-22.5°-135°$.

The height of this triangle is:

$$\dfrac{p}{2} \cdot \tan(22.5°)$$

$$= \dfrac{\sqrt{2} - 1}{4} (\sqrt{2} - 1)$$
$$= \dfrac{3 - 2\sqrt{2}}{4}$$

The area of the cookie is the area of the isosceles right triangle on the left, the parallelogram on the right, and the small isosceles triangle in the center.
$$Area = \Bigg(\dfrac{(2p)^2}{2} + n \cdot q + \dfrac{p \cdot h}{2}\Bigg)$$
$$= \Bigg(\dfrac{(\sqrt{2} - 1)^2}{2} + (\sqrt{2} - 1)\Big(\dfrac{2 - \sqrt{2}}{4}\big) + \Big(\dfrac{\sqrt{2} - 1}{4}\Big)\Big(\dfrac{3 - 2\sqrt{2}}{4}\Big)\Bigg)$$
$$= \Bigg(\dfrac{3 - 2\sqrt{2}}{2} + \dfrac{3\sqrt{2} - 4}{4} + \dfrac{5\sqrt{2}-7}{16}\Bigg)$$
$$= \Bigg(\dfrac{24 - 16\sqrt{2}+ 12\sqrt{2} - 16 + 5\sqrt{2} - 7}{16}\Bigg)$$
$$ = \dfrac{\sqrt{2} + 1}{16} \approx 0.1509$$
Three cookies out of the dough yields:
$$\dfrac{3 \cdot 0.1509}{0.5} \approx 90.5\%$$.

Extra Credit

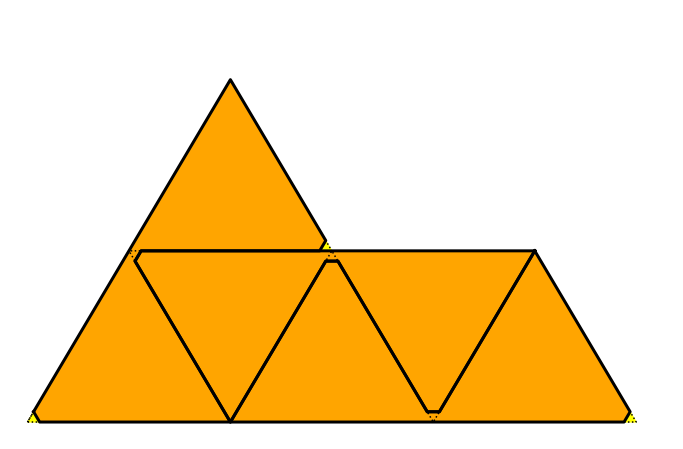
For the sphinx, the following picture has the maximum cookie area by three identical shapes within the dough.

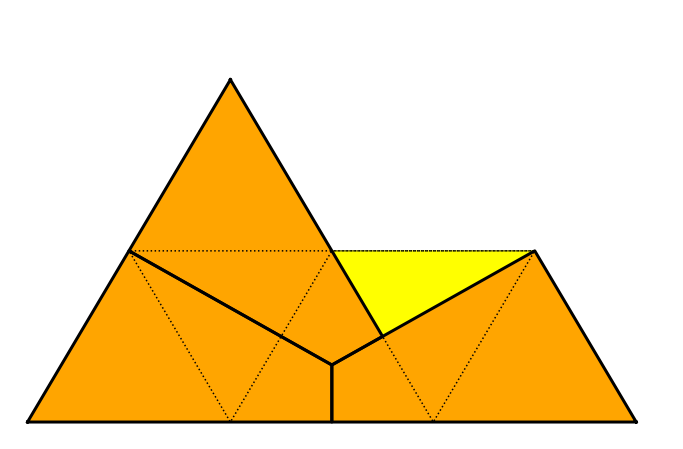
Answer

Only half of one of the six equilateral triangles is unused dough:
$$\dfrac{5.5}{6} \approx 91.7\%$$.

Update

I realized two days later than the answer approaches 100%. :(

Rohan Lewis

2020.12.07 (Updated 2020.12.09)

Code can be found here