Can You Pass the Cranberry Sauce?

Riddler Classic

From Patrick Lopatto comes a riddle we can all be thankful for:

To celebrate Thanksgiving, you and 19 of your family members are seated at a circular table (socially distanced, of course). Everyone at the table would like a helping of cranberry sauce, which happens to be in front of you at the moment.

Instead of passing the sauce around in a circle, you pass it randomly to the person seated directly to your left or to your right. They then do the same, passing it randomly either to the person to their left or right. This continues until everyone has, at some point, received the cranberry sauce.

Of the 20 people in the circle, who has the greatest chance of being the last to receive the cranberry sauce?

Solution

Let us look at this problem in a more general form. Assume $n$ people are sitting at a circular table. At any point in this procedure, exactly $m$ people, $1 \leq m \leq n$ have been sauced, that is, have received the bowl of cranberry sauce, and $n-m$ are waiting. A diagram below illustrates the saucing.

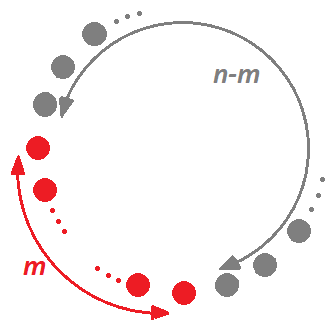
Once $m$ people are sauced, the most recent individual sauced who is holding the bowl is either on the far left or far right of the arc of those who have been sauced.

Proof I.

The next new recepient is either the one immediately to the far left or far right of the arc. The probabilities of them being the next new recepient will be shown to be as illustrated below.

True for $m = 1$.

Notice in the beginning when you hold the cranberry sauce, the individuals immediately to your left and right have equal probabilities of being the next new recepient. $$\frac{m}{m+1} = \frac{1}{m+1} = \frac{1}{2}$$

Assume $m = k$.

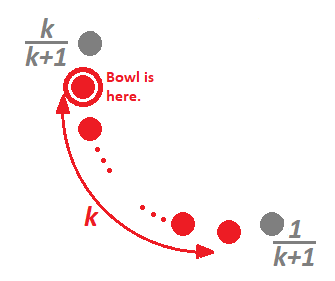
For $m = k + 1$.

This diagram is achieved from $m=k$ where the cranberry sauce is passed left around the circle.

The $k+1$ who have been sauced are labeled as two groups of $k$, differing only by their endpoints. Note the dark green $k$ is the sauced group from $m=k$.

From where the bowl is currently located, the probability of the individual to the left being the next new recepient is $\dfrac{k}{k+1}$, as long as the sauce is passed within the light green. The probability of being passed to the rightmost individual in the dark green $k$ from the current bowl location is $\dfrac{1}{k+1}$. From this rightmost position in the dark green $k$, getting back to the current bowl location is also $\dfrac{1}{k+1}$. This repeats.

Thus, the probability from the current bowl location to the individual immediately to the left being the next new recipient is:

$$\frac{k}{k+1} + \frac{k}{(k+1)^3} + \frac{k}{(k+1)^5} + \cdots$$

$$= \frac{k}{k+1} \bigg(1 + \frac{1}{(k+1)^2} + \frac{1}{(k+1)^4} + \cdots\bigg)$$
$$= \dfrac{\dfrac{k}{k+1}}{1 -\dfrac{1}{(k+1)^2}}$$
$$= \dfrac{\dfrac{k}{k+1}}{\dfrac{(k+1)^2 - 1}{(k+1)^2}}$$
$$= \frac{k}{k+1} \cdot \frac{(k+1)^2}{(k^2 +2k)}$$
$$= \frac{k+1}{k+2}$$

From the current bowl location, it follows that the probability of the individual immediately to the right of the sauced arc will be the next new recepient is $\dfrac{1}{k+2}$.

Note that the probabilities of the two possible next new recipients would be switched if the bowl were at the far right of the sauced arc.

Proof II.

Note that from the initial description, there are $m$ possibilities for exactly $m$ individuals to have been sauced. This is because you could be in any of the $m$ positions. It will be shown that each of these scenarios is equally likely with probability $\dfrac{1}{m}$.

In addition, the cranberry sauce bowl could be with the most recent new recepient at either end of the sauced arc. The two exceptions are the two scenarios where you are at an end. The probabilities of the location of the cranberry sauce depends on the location of where you are in the sauced arc.

$i$ represents the number of sauced individuals to the right of you. These probabilities will be shown to be as illustrated below.

True for $m = 2$.

For $i = 0$, $\dfrac{m-i-1}{m-1} = 1$ and $\dfrac{i}{m-1} = 0$.

For $i = 1$, $\dfrac{m-i-1}{m-1} = 0$ and $\dfrac{i}{m-1} = 1$.

From the description, we know each of these is equally likely with probability $\dfrac{1}{2}$.

Assume $m = k$.

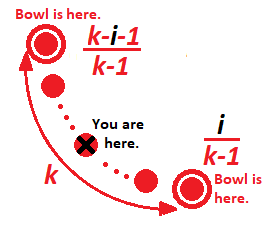
$k$ scenarios, for $0 \leq i \leq k-1$, each equally likely with probability $\dfrac{1}{k}$.

For $m = k + 1$.

For a sauced arc of $k+1$ individuals, we will look at the two possibilities of the bowl being at the left most and right most ends of the arc.

Case 1 (Left most):

Using $m = k$ above and the probabilities from Proof I. for the next new recepient, the above illustration above can be achieved by:

(One of the $k$ locations for you) x (Left most of sauced arc and next new recepient being left + Right most of sauced arc and next new recepient being left)

$$ = \frac{1}{k} \cdot \bigg(\frac{k-i-1}{k-1} \cdot \frac{k}{k+1} + \frac{i}{k-1} \cdot \frac{1}{k+1}\bigg)$$

$$ = \frac{1}{k} \cdot \bigg(\frac{k^2-ik-k+1}{(k-1)(k+1)}\bigg)$$
$$ = \frac{(k-i)(k-1)}{(k-1)k(k+1)}$$
$$ = \frac{(k-i)}{k} \cdot \frac{1}{k+1}$$
$$ = \frac{((k+1)-i-1)}{(k+1)-1} \textrm{ with probability of }your\textrm{ location being } \frac{1}{k+1}$$

Case 2 (Right most):

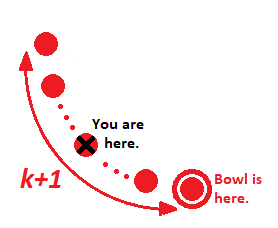
In this case, because the next new recepient will be to the right of you, $i$ changes. $i-1$ will be looked at for $m=k$ in order to achieve $i$ for $m=k+1$ in this case.

(One of the $k$ locations for you) x (Left most of sauced arc and next new recepient being right + Right most of sauced arc and next new recepient being right)

$$ = \frac{1}{k} \cdot \bigg(\frac{k-(i-1)-1}{k-1} \cdot \frac{1}{k+1} + \frac{(i-1)}{k-1} \cdot \frac{k}{k+1}\bigg)$$

$$ = \frac{1}{k} \cdot \bigg(\frac{(i-1)k+k-(i-1)-1}{(k-1)(k+1)}\bigg)$$
$$ = \frac{i(k-1)}{(k-1)k(k+1)}$$
$$ = \frac{i}{k}\cdot \frac{1}{k+1}$$
$$ = \frac{i}{(k+1)-1} \textrm{ with probability of }your\textrm{ location being } \frac{1}{k+1}$$

Note that when $i = 0$, all other sauced individuals are to your left and Case 1 yields $1$ and Case 2 yields $0$.

Similarly, when $i = k$, all other sauced individuals are to your right and Case 1 yields $0$ and Case 2 yields $1$.

If $m = n-1$, there are $m$ scenarios, each with probability $\dfrac{1}{m}$, and one person is remaining to be sauced.

Therefore, for $n$ people, everyone besides you has an equal chance of $\dfrac{1}{n-1}$ to be the last to receive the cranberry sauce.

Answer

For $n = 20$, everyone besides you has an equal probability of $\dfrac{1}{19}$ to be the last to receive the cranberry sauce.

Rohan Lewis

2020.11.23