Visualization and Statistical Analysis with Housing for Boston, MA

Final for Statistics for Data Science with Python

Rohan Lewis

2020.04.03

Complete code can be found here. Click graphs and plots for full size.

I. Objective

I am using the Boston, Massachusetts dataset from the class notes. This dataset contains 506 observations and 13 variables related to house sales in Boston, Massachusetts. The variables are related to characteristics and measurements of the houses, their locations, and purchases.

Refer to the description for a complete list of variables and labels.

I was given specific questions and prompts related to exploratory data analysis visualizations and statistical testing.

II. EDA Visualizations

1) Median Value of Owner-Occupied Homes

About half of the median values lie between ~\$17,000 and ~$25,000. There are several expensive median value neighborhoods, as shown by the outliers.

2) Charles River

The vast majority of neighborhoods are not adjacent to the Charles River.

3) Median Value of Owner-Occupied Homes vs Home Ages

As a general rule, the percent of old houses corresponds with an overall decreased median value. However, there are a few select neighborhoods of high median values, as shown by the outliers.

4) Nitric Oxide Concentrations vs Proportion of Non-Retail Business Acres

There is a clear positive relationship with nitrix oxide concentrations and % of non-retail business acres. It is not particularly weak or strong, but noticeable.

5) Pupil to Teacher Ratio

The distribution of pupil to teacher ratio is skewed left.

III. Statistical Analysis

Complete test results can be found here.

1) Median Value of Owner-Occupied Homes and Charles River

Hypothesis:

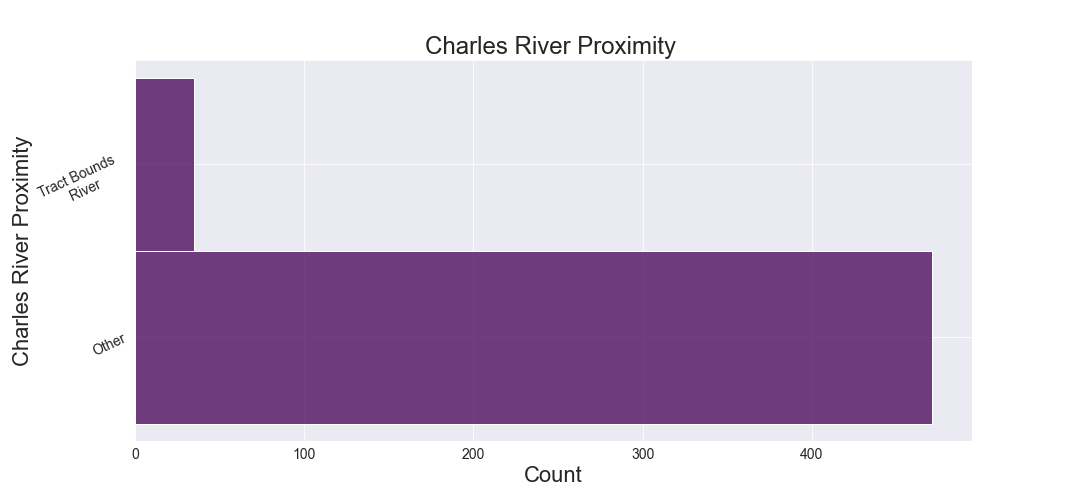
The median value of houses bounded by the Charles River is different from that of those which are not.

H₀:

$M_{CR} = M_{0}$

H_A:

$M_{CR} ≠ M_{0}$

Conclusion

The Levene Test was first run to determine equality of variances of the median value houses bounded by the Charles River and that of those which are not. The $\text{p-value} = 0.003 < 0.05$, so we can assume unequal variances.

Running the T-test for Independent Samples, the $\text{p-value} = 7.39 * 10 ^{-5} < 0.05$. The null hypothesis is rejected as there is significant evidence that the median value of houses bounded by the Charles River is different from that of those which are not.

2) Median Value of Owner-Occupied Homes and Home Ages

Hypothesis:

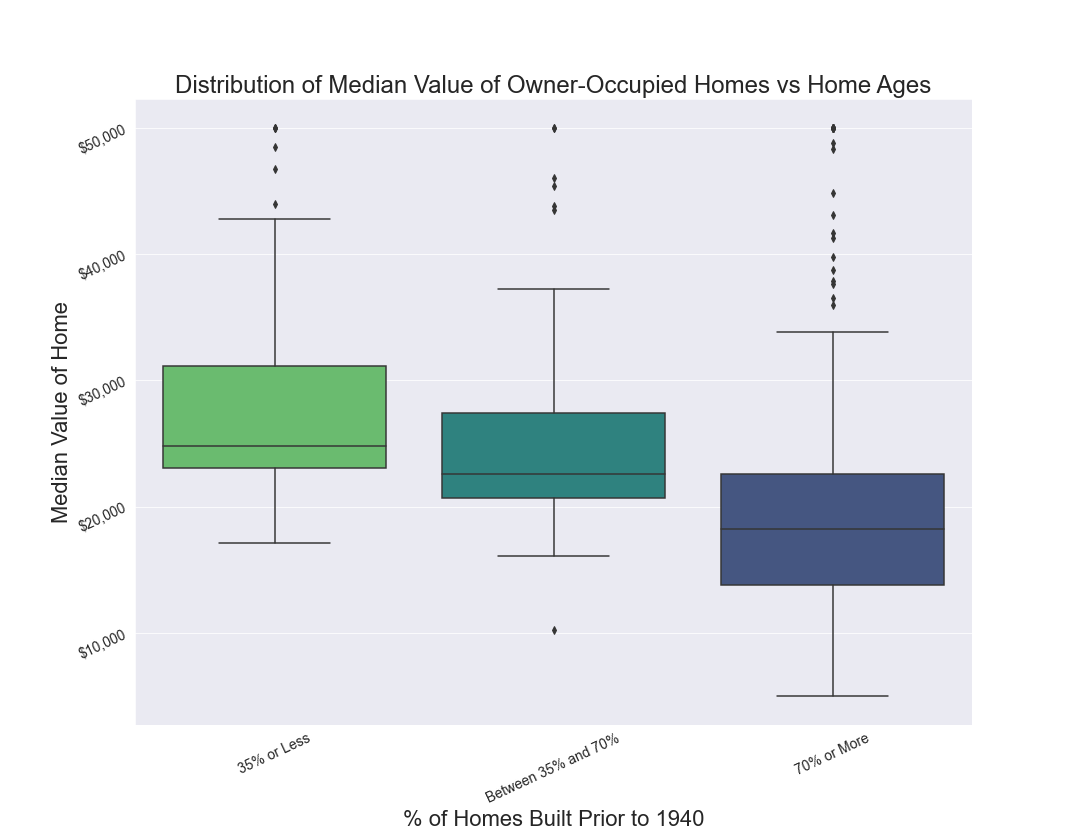
The median value of houses, depending on the proportion of houses built prior to 1940, are different.

H₀:

$M_{35} = M_{35-70} = M_{70}$

H_A:

$M_{35} ≠ M_{35-70}$ or
$M_{35-70} ≠ M_{70}$ or
$M_{70} ≠ M_{35}$

Conclusion

The Levene Test was first run to determine equality of variances of the median value houses, depending on the proportion of houses built prior to 1940. The $\text{p-value} = 0.063 > 0.05$, so we can assume equal variances among t he three groups.

Running the ANOVA, the $\text{p-value} = 1.71 * 10 ^{-15} < 0.05$. The null hypothesis is rejected as there is significant evidence that the median value of houses is different between at least one pair of the groups split by proportion of houses built prior to 1940.

3) Nitric Oxide Concentrations and Proportion of Non-Retail Business Acres

Hypothesis:

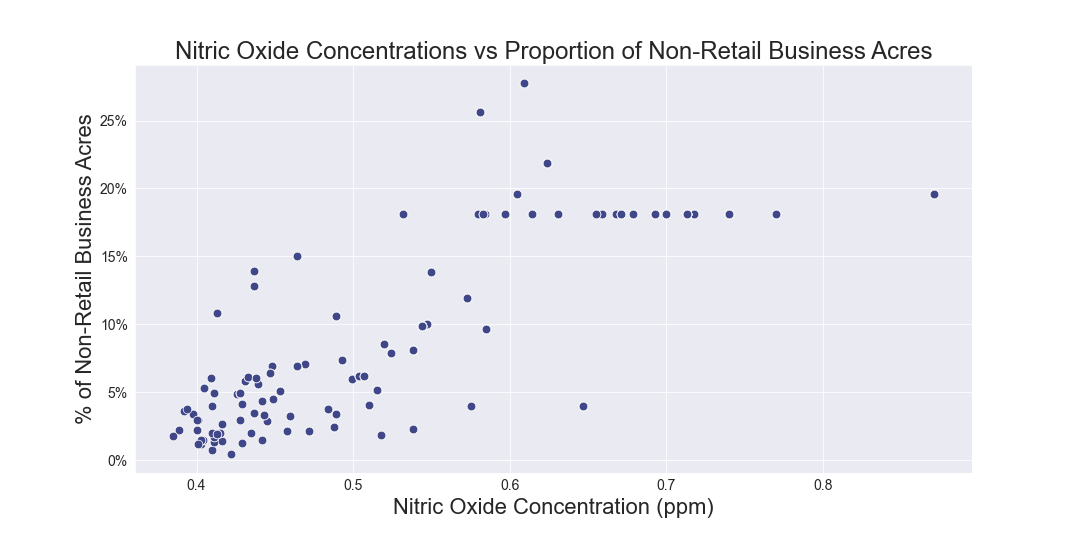
There is no relationship between Nitric Oxide concentrations and the proportion of non-retail business acres per town.

H₀:

Nitric oxide is not correlated with proportion of non-retail business acres.

H_A:

Nitric oxide is correlated with proportion of non-retail business acres.

Conclusion

Running the Pearson Correlation Test, the $\text{p-value} = 7.91 * 10 ^{-98} < 0.05$. The null hypothesis is rejected as there is significant evidence that nitric oxide is correlated with proportion of non-retail business acres.

4) Weighted Distance to Boston Employment Centres and Median Value of Owner-Occupied Homes

Hypothesis:

The weighted distance to the five Boston employment centres impacts the median value of owner-occupied homes.

H₀:

$m = 0$.

H_A:

$m ≠ 0$.

Conclusion

Running Regression Analysis, the $\text{p-value} = 1.21 * 10 ^{-8} < 0.05$. The null hypothesis is rejected as there is significant evidence that the weighted distance to the five Boston employment centres impacts the median value of owner-occupied homes.

Furthermore, an additonal weighted distance increases the median value by $\$1,091.61$.