Can You Brighten Up the Room?¶

Fiddler¶

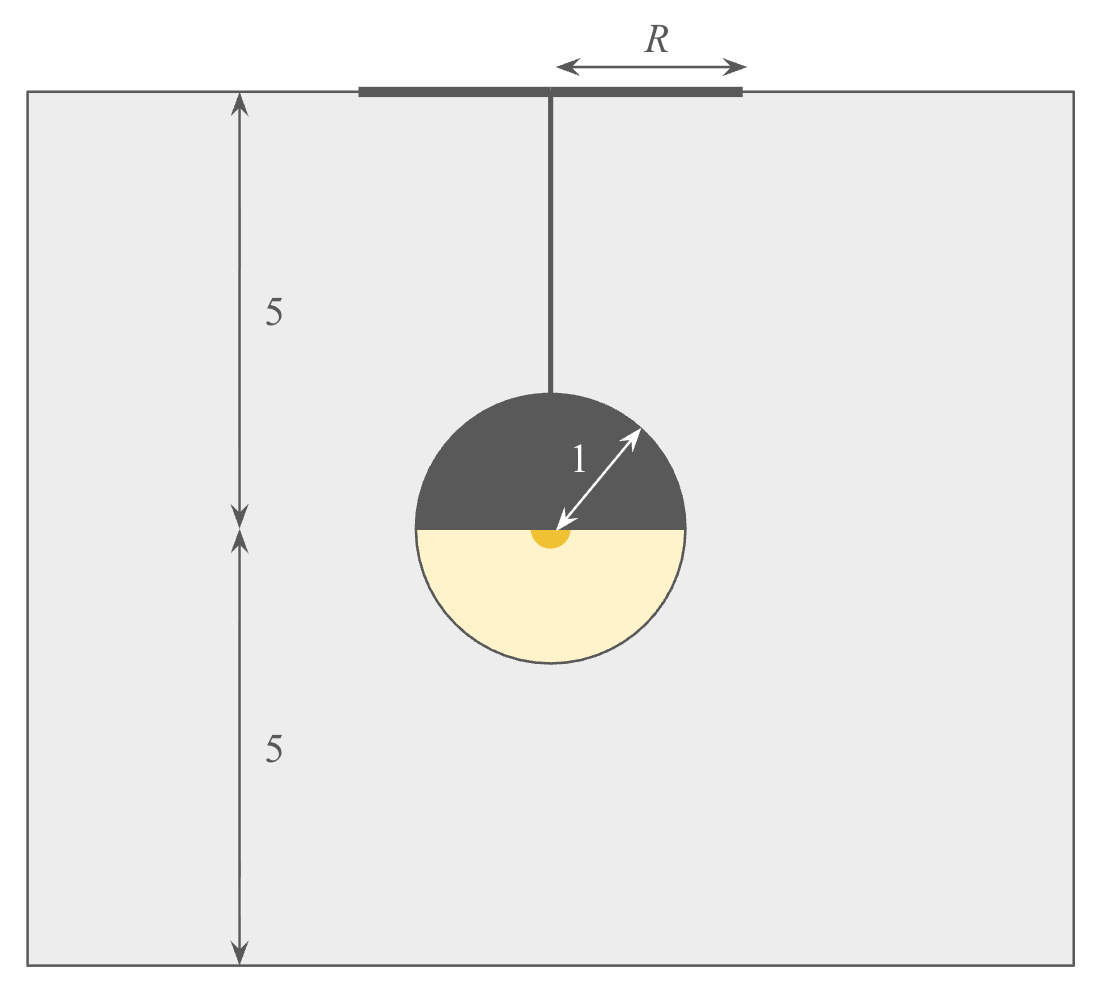
While dining at a restaurant, I notice a lamp descending from the ceiling, as shown in the diagram below. The lamp consists of a point light source at the center of a spherical bulb with a radius of 1 foot. The top half of the sphere is opaque. The bottom half of the sphere is semi-transparent, allowing light out (and thus illuminating my table) but not back in. The light source itself is halfway up to the ceiling—5 feet off the ground and 5 feet from the ceiling. The ground reflects light.

Above the light, on the ceiling, I see a circular shadow. What is the radius R of this shadow?

Solution¶

I considered the general case first.

From the diagram above:

  • $AB = BC = IJ = JD = HF = h$
  • $BE = r$
  • $AG = R$

The beam of light as a result of $\angle{CBD}$ defines the radius of the shadow $R$, as when reflected at $D$, $DG$ is tangent to $\bigcirc B$ at $E$.

$$\triangle DJB \cong \triangle DJF \cong \triangle FHG$$

It follows that,

$$AI = BJ = IH = JF = HG = \frac{R}{3}$$

In right $\triangle BEF$,

  • $BE = r$
  • $BF = \frac{2R}{3}$
  • Thus, $EF = \sqrt{\frac{4}{9}R^2 - r^2}$

In right $\triangle DJF$,

  • $DJ = h$
  • $JF = \frac{R}{3}$
  • Thus, $DF = \sqrt{h^2 + \frac{1}{9}R^2}$

Because $\angle BFD$ is common between the right $\bigtriangleup$s,

$$\triangle BEF \sim \triangle DJF$$

Any proportion from the sides of these two can be created to relate $h$, $r$, and $R$.
\begin{align*} \dfrac{BF}{BE} &= \dfrac{DF}{DJ} \\ \dfrac{\frac{2R}{3}}{r} &= \dfrac{\sqrt{h^2 + \frac{1}{9}R^2}}{h} \\ \dfrac{2hR}{3r} &= \sqrt{h^2 + \frac{1}{9}R^2} \\ \dfrac{4h^2R^2}{9r^2} &= h^2 + \frac{1}{9}R^2 \\ 4h^2R^2 &= 9h^2r^2 + r^2R^2 \\ \end{align*}

Thus,

$$\boxed{R = \dfrac{3hr}{\sqrt{4h^2-r^2}}}$$

Answer¶

Given $h = 5$ and $r = 1$,

$$\boxed{R = \dfrac{5}{\sqrt{11}} \approx 1.508\text{ feet}}$$

Extra Credit¶

Now suppose the lamp has a radius r and is suspended a height h off the ground in a room with height 2h. Again, the radius of the shadow on the ceiling is R.

For whatever reason, the restaurant’s architect insists that she wants r, h, and R, as measured in feet, to all be whole numbers. What is the smallest value of R for which this is possible?

Solution¶

Using code, the smallest value of $R$ I determined were with $h = 52\text{ feet}$ and $r = 40\text{ feet}$.

$$\boxed{R = 65\text{ feet}}$$

Rohan Lewis¶

2026.01.19¶

Code can be found here.