Can You Topple the Tower?

Fiddler

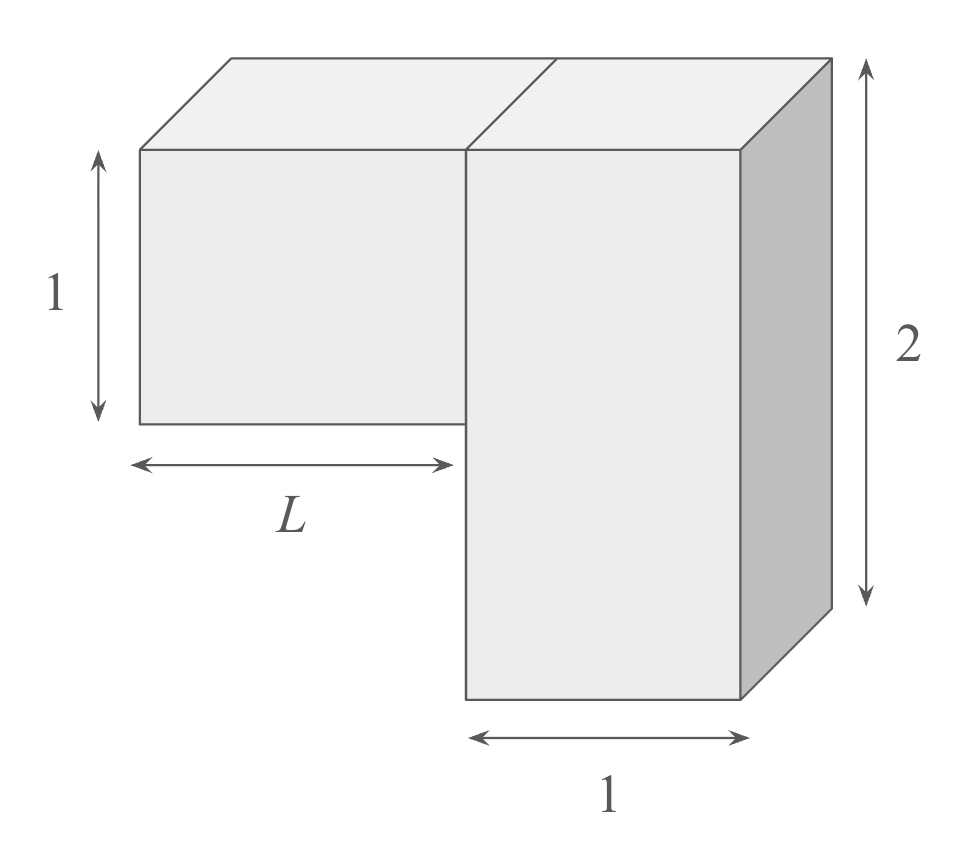
A block tower consists of a solid rectangular prism whose height is 2 and whose base is a square of side length 1. A second prism, made of the same material, and with a base that’s L by 1 and a height of 1, is attached to the top half of the first block, resulting in an overhang as shown below.

When L exceeds some value, the block tower tips over. What is this critical length L?

Solution

Depth can be ignored.

Place the left bottom corner of the block tower at $(1, 0)$. Its center is at $\big(\frac{3}{2}, 1\big)$ and its weight is 2.

The second prism has its center at $\big(1-\frac{L}{2}, \frac{3}{2}\big)$ and its weight is $L$.

The center of mass of the entire prism is thus,

\begin{align*} =& \left(\dfrac{2\cdot\frac{3}{2}+L\cdot\left(1-\frac{L}{2}\right)}{2+L}, \dfrac{2\cdot 1 + L\cdot\left(\frac{3}{2}\right)}{2+L}\right) \\ =& \left(\dfrac{-\frac{L^2}{2} + L + 3}{2+L}, \dfrac{\frac{3}{2}L + 2}{2+L}\right) \\ \end{align*}

When the x-value passes over $x = 1$, the tower will tip over.

\begin{align*} 1 = & \dfrac{-\frac{L^2}{2} + L + 3}{2+L} \\ 2+L =& -\frac{L^2}{2} + L + 3 \\ \frac{L^2}{2} =& 1 \\ \end{align*}

Answer

$$\boxed{L = \sqrt{2}}$$

Extra Credit

Instead of rectangular prisms, now suppose the tower is part of an annulus. More specifically, it’s the region between two arcs of angle 𝜽 in circles of radius 1 and 2, as shown below.

For small values of 𝜽, the tower balances on one of its flat sides. But when 𝜽 exceeds some value, the tower no longer balances on a flat side. What is this critical value of 𝜽?

Solution

The center of mass is
$$\left(\frac{M_y}{M}, \frac{M_x}{M}\right)$$
Where the total mass is,
$$M = \int \int\limits_R r \cdot dr \cdot d\alpha$$
and moments are $$M_x = \int \int\limits_R y \cdot r \cdot dr \cdot d\alpha = \int \int\limits_R r^2\cdot\sin\alpha \cdot dr \cdot d\alpha$$
and
$$M_y = \int \int\limits_R x \cdot r \cdot dr \cdot d\alpha = \int \int\limits_R r^2\cdot\cos\alpha \cdot dr \cdot d\alpha$$

From the given information, $0 \le \alpha \le \theta$ and $1 \le r \le 2$.

\begin{align*} M &= \int\limits_{\alpha = 0}^\theta \int\limits_{r = 1}^2 r \cdot dr \cdot d\alpha \\ &= \int\limits_{\alpha = 0}^\theta \left[\frac{r^2}{2}\right]_1^2 \cdot d\alpha \\ &= \frac{3}{2} \cdot \int\limits_{\alpha = 0}^\theta d\alpha = \boxed{\frac{3}{2}\theta} \\ \end{align*}

Solving for the moments, $M_x$ and $M_y$

\begin{align*} M_x &= \int\limits_{\alpha = 0}^\theta \int\limits_{r = 1}^2 r^2 \sin\theta \cdot dr \cdot d\alpha \\ &= \int\limits_{\alpha = 0}^\theta \sin\alpha \cdot \left[\frac{r^3}{3}\right]_1^2 \cdot d\alpha \\ &= \frac{7}{3} \cdot\int\limits_{\alpha = 0}^\theta \sin\alpha \cdot d\alpha = \boxed{\frac{7}{3}\left(1 - \cos\theta\right)}\\ \end{align*}\begin{align*} M_y &= \int\limits_{\alpha = 0}^\theta \int\limits_{r = 1}^2 r^2 \cos\theta \cdot dr \cdot d\alpha \\ &= \int\limits_{\alpha = 0}^\theta \cos\alpha \cdot \left[\frac{r^3}{3}\right]_1^2 \cdot d\alpha \\ &= \frac{7}{3} \cdot\int\limits_{\alpha = 0}^\theta \cos\alpha \cdot d\alpha = \boxed{\frac{7}{3}\sin\theta}\\ \end{align*}

The center of mass for some $\theta$ is

$$\boxed{\left(\frac{14\sin\theta}{9\theta}, \frac{14\left(1 - \cos\theta\right)}{9\theta}\right)}$$

Again, when the x-value passes over $x = 1$, the tower will tip over.

Using Wolfram Alpha,

$$14\sin\theta = 9\theta$$

when

$$\boxed{\theta \approx 1.55537}$$

Answer

$$\boxed{1.55537 \text{ radians} \approx 89.116^\circ}$$

Rohan Lewis

2025.12.15

Code can be found here.