Solution¶
I noticed that angles of the form $\frac{360}{n}$, the exterior angle of a regular $n$-gon make parallel paths.
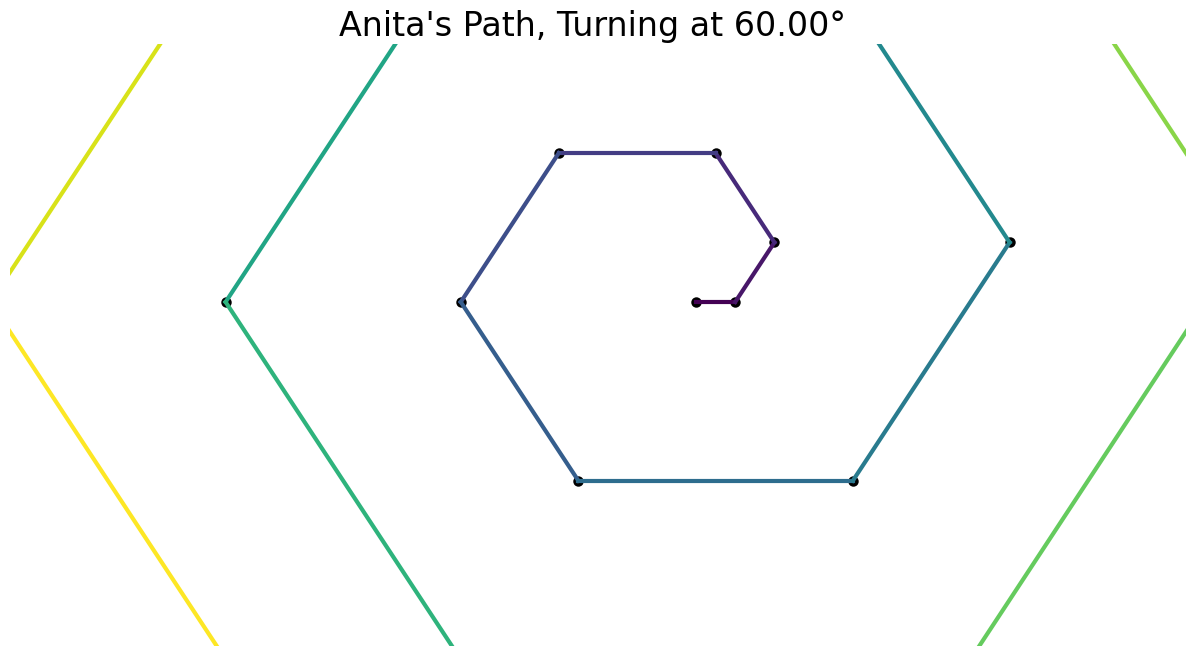
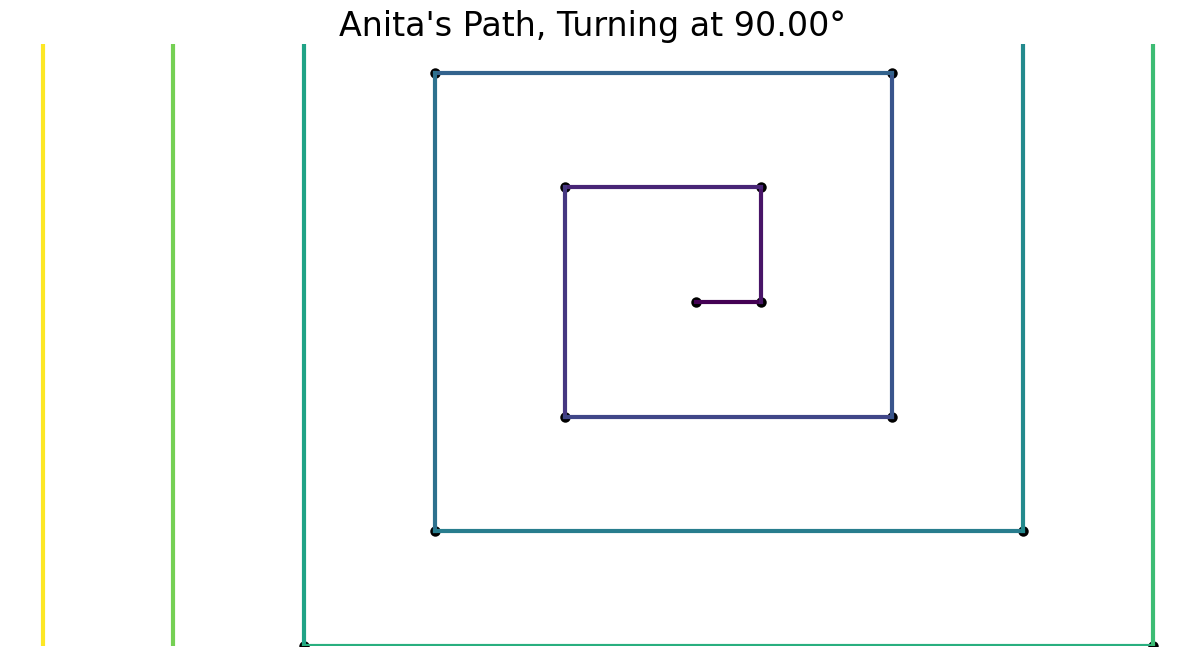
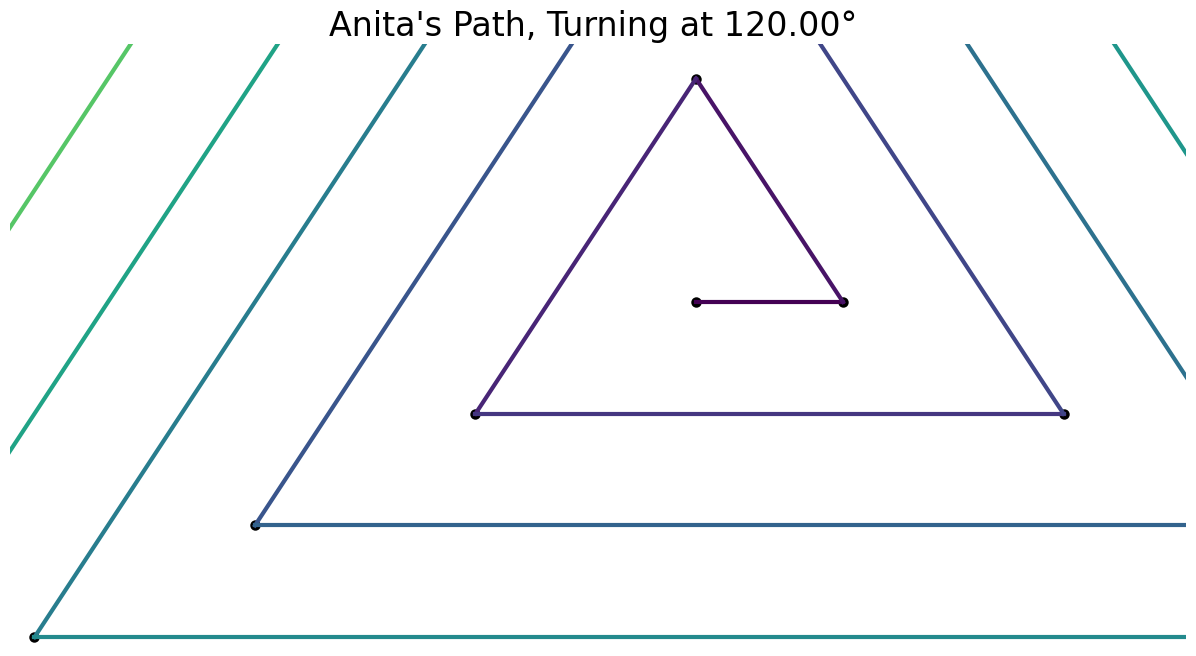
It was pretty clear to me that the 4-inch side would be the first to cross over the 1-inch side.
Anita the ant is going for a walk in the sand, leaving a trail as she goes. First, she walks 1 inch in a straight line. Then she rotates counterclockwise by an angle ๐, after which she walks another 2 inches. She rotates counterclockwise an angle ๐ again, after which she walks 3 inches. She keeps doing this over and over again, rotating counterclockwise an angle ๐ and then walking 1 inch farther than she did in the previous segment.
At some point during her journey, she crosses over her initial 1-inch segment. By โcross over,โ I am including the two end points of that first segment.
Anita realizes that ๐ was the smallest possible angle such that she crossed over her 1-inch segment. (Among the ants, sheโs known for her mathematical prowess.)
How long was the segment along which she first crossed over the 1-inch segment? Your answer should be a whole number of inches.
I noticed that angles of the form $\frac{360}{n}$, the exterior angle of a regular $n$-gon make parallel paths.
It was pretty clear to me that the 4-inch side would be the first to cross over the 1-inch side.
The 4-inch side.
Itโs time for you to check Anitaโs work. What was the measure of angle ๐?
Remember, this was the smallest possible angle for each turn such that she crossed over her 1-inch segment at some later point.
Since angles are congruent, the triangle created is isoceles.
\begin{align*} \cos (180^\circ - \phi) &= \frac{\frac{3}{2}}{2} \\ 180^\circ - \phi &= \cos^{-1} \left(\frac{3}{4}\right) \\ \phi &= 180^\circ - \cos^{-1} \left(\frac{3}{4}\right) \\ \end{align*}The first intersection to occur for any line happens as soon as the angle is obtuse, or $\phi \gt 90^\circ$. I would like to think that this is not a difficult proof. This image of $90.5^\circ$ provides some context.
$135^\circ$ has many intersections in a fascinating pattern.
I created two videos, one close up and one a little zoomed out. It is impossible to capture infinity, but these provide an idea!