Can You Box the Letters?

Fiddler

In the game of Letter Boxed from The New York Times, you must connect letters together around a square to spell out words. However, from any given letter, the next letter cannot be on the same side of the square.

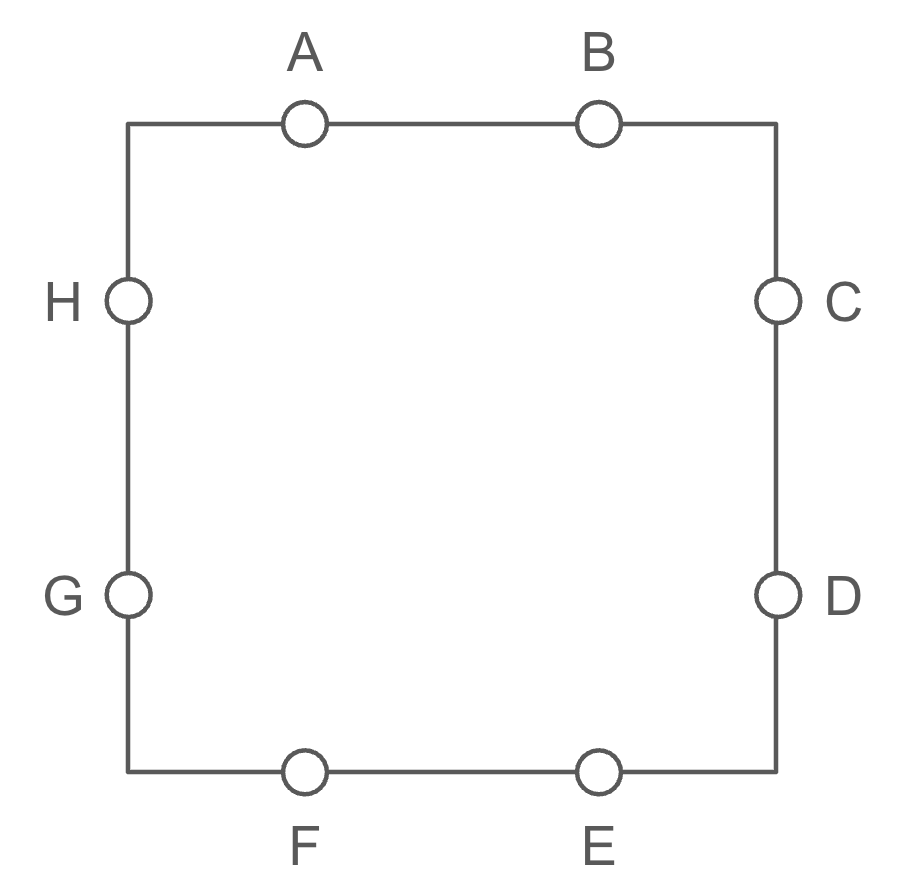
Consider the following diagram, which consists of eight points (labeled A through H), two on each side of the square. A valid “letter boxed” sequence starts at any of the eight points, and proceeds through all of the other points exactly once. However, adjacent points in the sequence can never be on the same side of the square. The first and last points in the sequence can be on the same side, but do not have to be.

As an illustration, AFBCHEDG is a valid sequence of points. However, AFBCHGED is not a valid sequence, since H and G are adjacent in the sequence and on the same side of the square.

How many distinct valid “letter boxed” sequences are there that include all eight points on the square?

Solution

I wrote code that did the following :

1. Create the array of letters.
2. Create a dictionary such that the keys are each letter and its values are valid possibilities for the next letter.
3. Create an empty list of sequences and an empty string for the current letter boxed.
4. LOOP : For each letter in the dictionary keys:
   1. Clone the dictionary and the current letter_boxed.
   2. Update the current letter boxed.
   3. Compare the letter boxed with the desired number of characters:
      1. If it matches :
         1. Save the string.
         2. Continue with next letter at LOOP.
      2. If it does not match :
         1. Get the possible next letters from the current letter.
         2. Remove the current letter from the dictionary.
         3. If it is empty :
            1. Continue with next letter at LOOP.
         4. If it is not empty :
            1. Remove the current letter as a next letter for all letters.
            2. Continue with the updated dictionary, updated next letter, and updated letter boxed string at LOOP.

Answer

The answer must be less than $8! = 40,320$.

My code gave me $13,824$.

Extra Credit

Instead of two points on each side of the square (and eight points in total), now there are three points on each side (and twelve points in total), labeled A through L in the diagram below.

How many distinct valid “letter boxed” sequences are there that include all 12 points on the square?

Answer

The answer must be less than $12! = 479,001,600$.

My code gave me $53,529,984$.

Rohan Lewis

2025.09.15

Code can be found here.