Every summer I try to run a cycling-related puzzle to coincide with the Tour de France. Previous puzzles have involved the team time trial, “King of the Mountain” points, the shape of the peloton, being paced up a climb, and last year’s catching the breakaway.
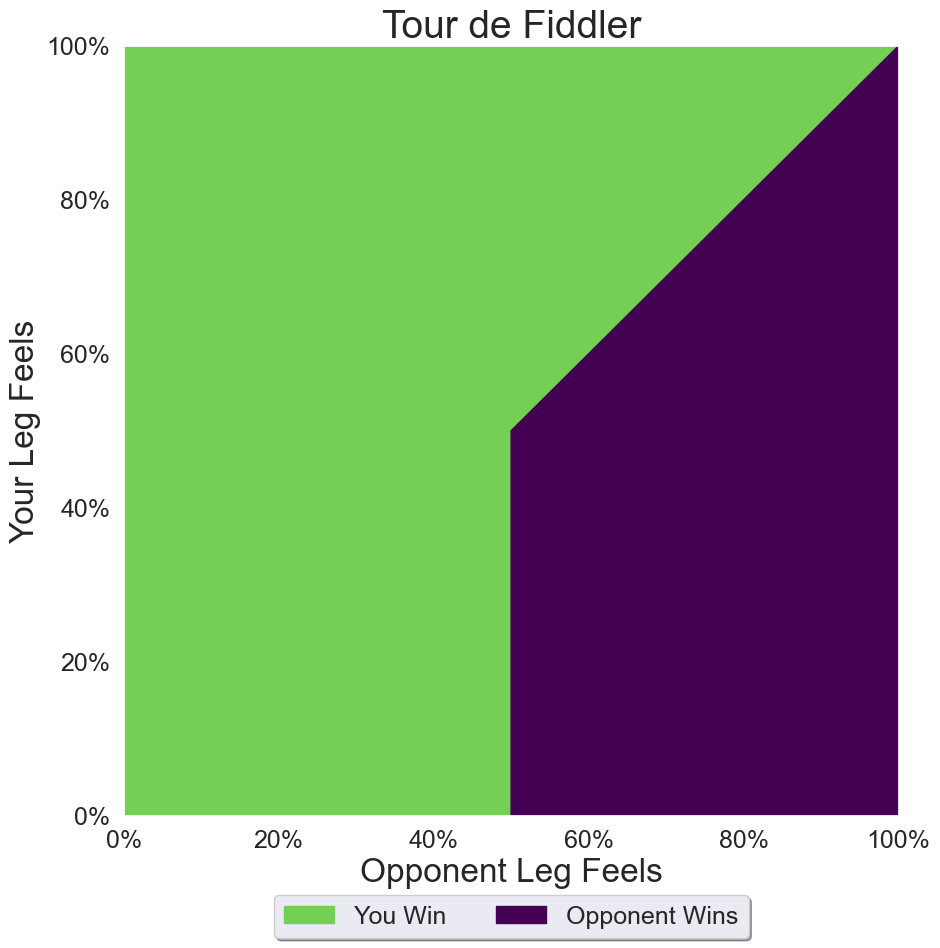
This time around, you and a competitor are approaching the finish of a grueling stage of the Tour de Fiddler. One of you will win the stage, the other will come in second. As you approach the finish, each of you will test the feeling of your legs, which will be somewhere between 0 percent (“I can barely go on!”) and 100 percent (“I can do this all day!”). For the purposes of this puzzle, these values are chosen randomly, uniformly, and independently.
Immediately after feeling your legs, you and your opponent each have a decision to make. Do you maintain your current pace, or do you sprint to the finish? Among those who sprint for the finish, whoever’s legs are feeling the best will win the stage. But if no one sprints for the finish, everyone has an equal chance of winning the stage. In the Tour de Fiddler, you must each decide independently whether to sprint for the finish based on your legs—you don’t have time to react to your opponent’s decision.
Normally, teams at the Tour de Fiddler keep their strategy and tactics close to the vest. But earlier today, your opponent’s manager declared on international television that if (and only if) your opponent’s legs were feeling 50 percent or better, they’d sprint for the finish.
As you are about to test your legs for the final sprint and see how they feel, what are your chances of winning the stage, assuming an optimal strategy?
There is no consequence of not sprinting, so you should always sprint.
You will win if both of you are feeling less than 50 percent. This is $\frac{1}{4}$ of the outcomes.
As long as one of you at least 50 percent, the probability of winning is equal between you and your opponent. $\frac{1}{2} \left(1 - \frac{1}{4}\right) = \frac{3}{8}$.
Instead of one opponent, now you have two—meaning three riders in total. As luck would have it, the managers for both other riders proclaimed that they’d sprint for the finish if (and only if) their legs were feeling 50 percent or better. Note that your opponents’ feelings are independent of each other.
As the three of you near the finish, your own team manager radios you the following message: “If your legs feel <garbled> percent or better, sprint for the finish!”
You can’t make out what the garbled part of the message is, and you’re too tired to radio back for confirmation. Instead, you somehow muster the energy to randomly, uniformly pick a number between 0 and 100 to fill in the blank from your manager’s message, thereby determining your racing strategy—optimization be damned!
Right before you choose your random strategy and test your legs, what are your chances of winning the stage against both opponents?
Similar to above, if all three riders are feeling less than 50 percent, you win, as you are the only one sprinting. This is $\frac{1}{8}$ of the outcomes.
As long as one of the three riders is at least 50 percent, the probability of winning is equal amongst all three riders. $\frac{1}{3} \left(1 - \frac{1}{8}\right) = \frac{7}{24}$.
The following 3D plot visualizes the sample space. (click for the interactive HTML)
For managers' thresholds of leg feels of $p$ or better with $n$ opponents, the probability that you have an advantage is $p^{n+1}$. Note that this is the (n+1)-dimensional cube of length $p$ about the origin in $n+1$ space in a (n+1)-dimensional cube of length 1.
As long as one of the $n+1$ riders feels at least $p$, the probability of winning is equal amongst all $n+1$ riders. $\frac{1}{n+1}(1−p^{n+1}) = \frac{1−p^{n+1}}{n+1}$
The probability of you winning is thus,
$$p^{n+1} + \frac{1−p^{n+1}}{n+1} = \boxed{\frac{n \cdot p^{n+1}+1}{n+1}}$$
