Answer¶
The maximum difference between scores occurs when both players drop exactly 110 pins. One player scores 110, the other player scores 290. The maximum difference is thus,
$$\boxed{180}$$
From Chris Payne comes a baffling bowling brainteaser:
In bowling, you roll a large, heavy ball toward a triangular array of 10 pins many feet away. You’d think the objective is to just knock down as many pins as possible. But thanks to the sport’s byzantine scoring system, it’s not that simple.
Bowling consists of 10 “frames,” and in each frame you have up to two chances to knock down the 10 pins. Your score for the frame is however many pins you knock down, but there are bonuses if you knock down all 10 pins:
If you knock down all 10 in one bowl, it’s called a strike. Your score for the frame is 10 plus however many pins you knock down in your next two bowls. Note that these next two bowls might occur in a single frame, or could be across the next two frames (if your very next bowl is again a strike).
If it takes you two bowls to knock down all 10 pins, it’s called a spare. Your score for the frame is 10 plus however many pins you knock down in your next one bowl.
Let’s look at a quick example. Suppose in frames 1 and 2 you bowl strikes, then in frame 3 you bowl a spare (three pins on the first bowl, seven on the second), and in frame 4 you knock down nine pins (five on the first bowl, four on the second). What’s your score?
Frame 1: 10 (from frame 1) + 10 (from frame 2) + 3 (from frame 3) = 23
Frame 2: 10 (from frame 2) + 3 (from frame 3) + 7 (from frame 3) = 20
Frame 3: 10 (from frame 3) + 5 (from frame 4) = 15
Frame 4: 9 (from frame 4)
So your total score on these four frames is 23 + 20 + 15 + 9 = 67. By my standards, that’s a pretty high score!
Something extra may be needed for the 10th and final frame. If you get a strike on the 10th frame, you get two extra rolls to determine your score for that frame. And if you get a spare, you similarly get a final roll to determine your score. The maximum score for a game is 300, earned from 12 consecutive strikes—10 strikes in the 10 frames, and then two additional strikes to compute the score for the 10th (and ninth) frame.
Now that we’ve reviewed how to score a game, let’s get to the actual puzzle!
If you knock down 100 pins over the course of a game, you are guaranteed to have a score that’s at least 100. But what’s the minimum total number of pins you need to knock down such that you can attain a score of at least 100?
Suppose someone only knocks down 0-10 pins in their first frame, and no other pins for the rest of the game. Their score is simply the number of pins they knocked down in their first frame.
Now, assume, whether by strike or spare, they knocked down 10 pins in the first frame. They also knock down a single pin in the first bowl of the second frame. That is one pin, but it counts for two points.
Maximizing strikes allows for more pins to be counted two or three times, thus minimizing the number of pins necessary for a particular score.
Suppose a bowler gets 4 strikes in the first four frames (or four consecutive frames),
Frame 1: 10 (from frame 1) + 10 (from frame 2) + 10 (from frame 3) = 30
Frame 2: 10 (from frame 2) + 10 (from frame 3) + 10 (from frame 4) = 30
Frame 3: 10 (from frame 3) + 10 (from frame 4) = 20
Frame 4: 10 (from frame 4) = 10
$40$ pins yields a score of $90$. Adding a few more pins knocked down will provide paths to yield at least 100.
Frame 1: 10 (from frame 1) + 10 (from frame 2) + 10 (from frame 3) = 30
Frame 2: 10 (from frame 2) + 10 (from frame 3) + 10 (from frame 4) = 30
Frame 3: 10 (from frame 3) + 10 (from frame 4) + $p$ (from frame 5) = 20 $+p$
Frame 4: 10 (from frame 4) + $p$ (from frame 5) + $q$ (from frame 5) = 10 $+p+q$
Frame 5: $p$ (from frame 5) + $q$ (from frame 5) = $p+q$
$40+p+q$ pins yields a score of $90+3p+2q$.
| p | q | Pins | Score |
|---|---|---|---|
| $4$ | $0$ | $44$ | $102$ |
| $3$ | $1$ | $44$ | $101$ |
| $2$ | $2$ | $44$ | $100$ |
At least four additional pins are needed.
$$\boxed{44 \text{ pins.}}$$From Chris Payne also comes some Extra Credit:
You and your opponent each play a single game in which you both knock down the same number of pins. However, your scores are quite different.
Your opponent remarks, “Given only the information that we knocked down the same number of pins in our two games, there’s no way the difference between our scores could have been any greater!”
What is this difference between your two scores?
A simple maximum score algorithm for a particular number of pins is to score all of those pins as early as possible in order to maximize strikes.
Scored once.
Scored twice.
Scored thrice.
Scored twice.
Scored once.
This yields,
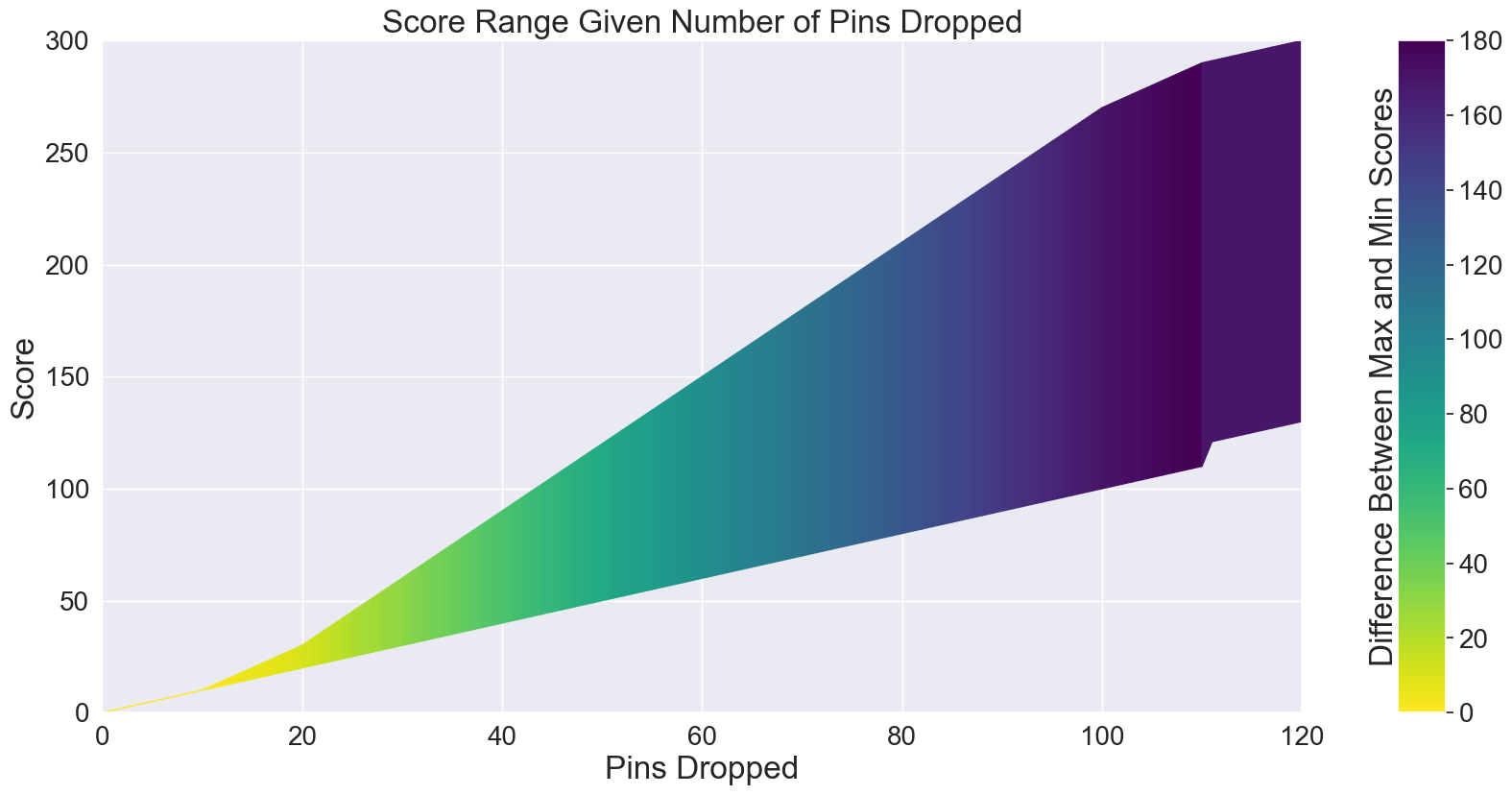
$$ Score_{max}(p) = \begin{cases} p, &0 \leq p \leq 10\\ 2p-10, &10 \lt p \leq 20\\ 3p-30, &20 \lt p \leq 100\\ 2p+70, &100 \lt p \leq 110\\ p+180, &110 \lt p \leq 120\\ \end{cases} $$For minimum score, simply avoid strikes and spares. While this is simple for up to 90 pins, which is a max of 9 pins per frame, strikes or spares are inevitable for pins 90 - 100.
A simple minimum score algorithm is to always miss all pins for the first bowl of each frame, and score up to 10 pins in the second bowl of each frame. If there is a resulting spare, this adds the pins scored in the next bowl, which is 0, as aforementioned.
The first 90 pins are therefore scored once.
Scored once if there are between 91 to 110 dropped pins.
Scored twice if there are between 111 to 120 dropped pins.
Since the spare in Frame 10 allows for an additional bowl, each pin dropped in Frame 11 will count for Frame 10's Score.
The Frame 11 pins are scored once.
In order to get to Frame 12, that means Frame 10 had a strike. Which means the pins in Frame 10 are scored twice, as there was a spare in Frame 9.
The Frame 12 pins are scored once.
This yields,
$$ Score_{min}(p) = \begin{cases} p, &0 \leq p \leq 110\\ p+10, &110 \lt p \leq 120\\ \end{cases} $$Combining the two functions yields,
$$ Score_{Diff}(p) = \begin{cases} 0, &0 \leq p \leq 10\\ p-10, &10 \lt p \leq 20\\ 2p-30, &20 \lt p \leq 100\\ p+70, &100 \lt p \leq 110\\ 170, &110 \lt p \leq 120\\ \end{cases} $$The maximum difference between scores occurs when both players drop exactly 110 pins. One player scores 110, the other player scores 290. The maximum difference is thus,
$$\boxed{180}$$
