Answer¶
Using Integral Calculator, the answer is
$$\frac{24}{\log_2{\frac{11}{5}}} \approx \boxed{21.0988 \text{ minutes}}$$
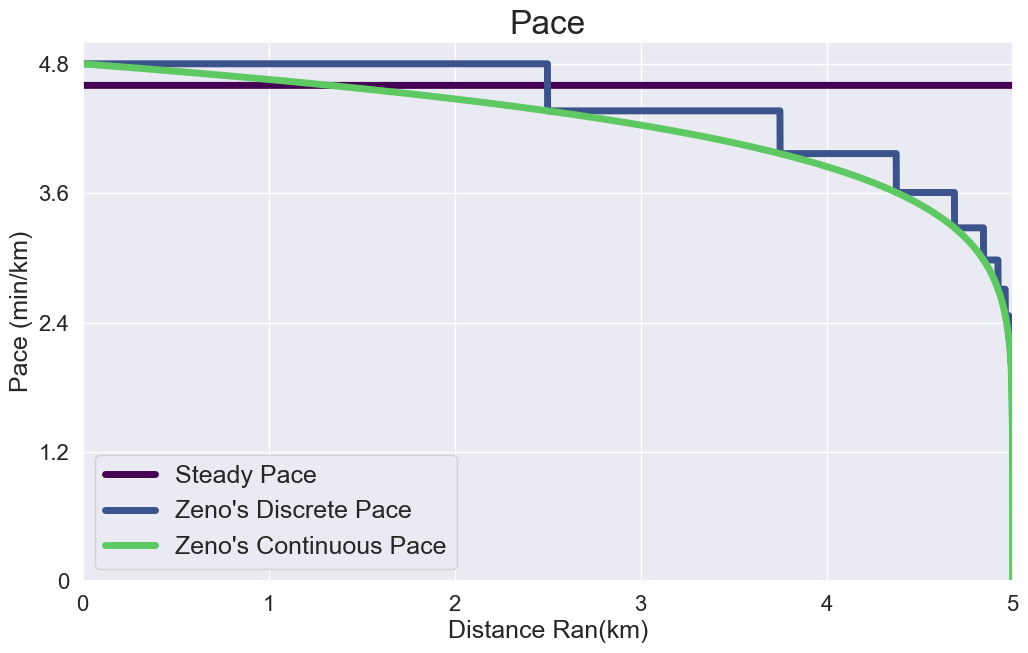
I’ve been experimenting with different strategies in 5000-meter races (known as “5K”s). If I run the distance at a steady pace, I’ll finish in precisely 23 minutes.
However, I tend to find a burst of energy as I near the finish line. Therefore, I’ve tried intentionally running what’s called a “negative split,” meaning I run the second half of the race faster than the first half—as opposed to a “positive split,” where I run a slower second half.
I want to take the concept of a negative split to the next level. My plan for an upcoming race—the “Zeno Paradox 5K”—is to start out with a 24-minute pace (i.e., running at a speed such that if I ran the whole distance at that speed, I’d finish in 24 minutes). Halfway through the race by distance (i.e., after 2500 meters), I’ll increase my speed by 10 percent. Three-quarters of the way through, I’ll increase by another 10 percent. If you’re keeping track, that’s now 21 percent faster than my speed at the start.
I continue in this fashion, upping my tempo by 10% every time I’m half the distance to the finish line from my previous change in pace. (Let’s put aside the fact that my speed will have surpassed the speed of light somewhere near the finish line.)
Using this strategy, how long will it take me to complete the 5K? I’m really hoping it’s faster than my steady 23-minute pace, even though I start out slower (at a 24-minute pace).
The initial speed is
$$\frac{5}{24} \text{km/min}$$
Start with
$$\text{speed} = \frac{\text{distance}}{\text{time}}\text{.}$$
Cross multiplying yields
$$\text{time} = \frac{\text{distance}}{\text{speed}}\text{.}$$
Since there are known discrete changing intervals of known distance and speed,
$$\text{time}_\text{Total} = \sum\limits_{n = 0}^{\infty} \frac{x_n}{s_n}$$
The interval distances, in kilometers, follow the geometric series: $\dfrac{5}{2}, \dfrac{5}{4}, \dots, \dfrac{5}{2^{n+1}}$
The corresponding interval speeds, in km/min, follow the geometric series: $\dfrac{5}{24}, \dfrac{5}{24}\left(\dfrac{11}{10}\right), \dots, \dfrac{5}{24}\left(\dfrac{11}{10}\right)^n$
Evaluating,
\begin{align*} \text{time}_\text{Total} &= \sum\limits_{n = 0}^{\infty} \frac{\dfrac{5}{2^{n+1}}}{\dfrac{5}{24}\left(\dfrac{11}{10}\right)^n} \\ \text{time}_\text{Total} &= \dfrac{5\cdot 24}{5\cdot 2}\sum\limits_{n = 0}^{\infty} \dfrac{1}{2^n}\left(\dfrac{10}{11}\right)^n \\ \text{time}_\text{Total} &= 12\sum\limits_{n = 0}^{\infty} \left(\dfrac{5}{11}\right)^n \\ \end{align*}
Evaluating the infinite geometric series,
\begin{align*}
\text{time}_\text{Total} &= 12 \cdot \frac{1}{1-\frac{5}{11}} \\
\text{time}_\text{Total} &= 12 \cdot \frac{11}{6} \\
\end{align*}
The total time will be $$\boxed{22 \text{ minutes.}}$$
I still want to run a negative split, but upping my tempo in discrete steps is such a slog. Instead, my next plan is to continuously increase my pace in the following way:
At the beginning of the race, I’ll start with a 24-minute pace. Then, wherever I am on the race course, I’m always running 10 percent faster than I was when I was twice as far from the finish line. Also, my speed should always be increasing in a continuous and smooth fashion.
(On the off chance you find more than one speed as a function of distance that satisfies all these conditions, I’m interested in seeing how. If only one such function exists, can you prove it? Regardless, my expectation is for the function to be as straightforward as possible.)
Using this strategy, how long will it take me to complete the 5K? Once again, I’m hoping it’s faster than my steady 23-minute pace, even though I started out slower.
I’m always running 10 percent faster than I was when I was twice as far from the finish line.
The following table summarizes discrete values every halfway point to the finish line
| Distance | Distance from finish line | Exponent ${\mathop{g}(5-x)}$ |
|---|---|---|
| $0$ | $5$ | $0$ |
| $\dfrac{5}{2}$ | $\dfrac{5}{2}$ | $1$ |
| $\dfrac{15}{4}$ | $\dfrac{5}{4}$ | $2$ |
| $\dfrac{35}{8}$ | $\dfrac{5}{8}$ | $3$ |
| $\cdots$ | $\cdots$ | $\cdots$ |
| $\dfrac{5*(2^n-1)}{2^n}$ | $\dfrac{5}{2^n}$ | $n$ |
| $x$ | $5-x$ | $-\log_2\left(1-\dfrac{x}{5}\right)$ |
Thus the instantaneous speed $s$ at a distance $x$ is
$$\boxed{s(x) = \frac{5}{24}\left(\dfrac{11}{10}\right)^{-\log_2\left(1-\frac{x}{5}\right)}}$$
Solving for time,
\begin{align*}
\text{time} &= \frac{\text{distance}}{\text{speed}} \\
\text{time}_\text{Total} &= \frac{1}{\int s(x)dx } \\
\text{time}_\text{Total} &= \int\limits_{x=0}^5 \dfrac{24}{5}\left(\dfrac{11}{10}\right)^{\log_2\left(1-\frac{x}{5}\right)} dx\\
\end{align*}
Using Integral Calculator, the answer is
$$\frac{24}{\log_2{\frac{11}{5}}} \approx \boxed{21.0988 \text{ minutes}}$$
