How Long Is the River?

Fiddler

From Seth Cohen comes a puzzle that lines up neatly:

Seth recently came across a phenomenon known as a "river”, where spaces between words diagonally align from one line of text to the next. The following text has an 11-line river in the middle—see if you can spot it!

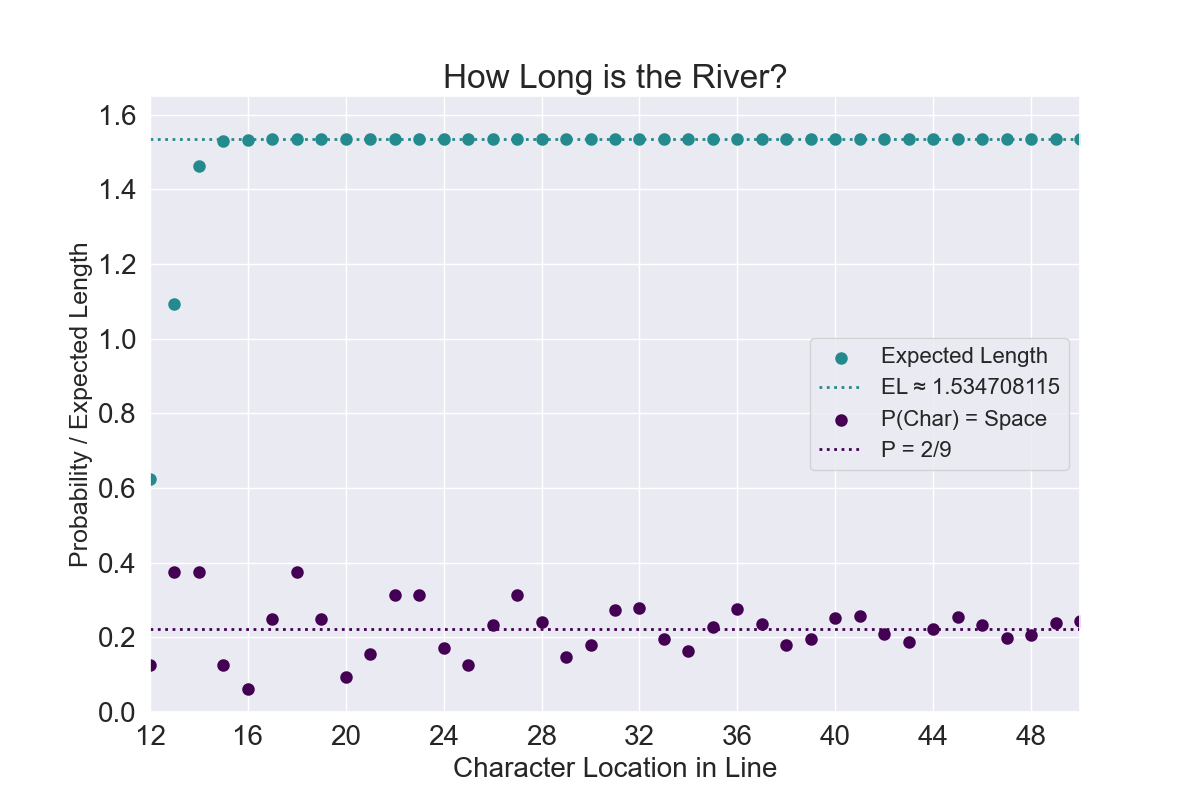
Before getting to rivers, let’s figure out where spaces are likely to appear in the (fictional) Fiddlish language, which includes only three- and four-letter words. These words are separated by spaces, but there is no other punctuation.

Suppose a line of Fiddlish text is generated such that each next word has a 50 percent chance of being three letters and a 50 percent chance of being four letters.

Suppose a line has many, many, many words. What is the probability that any given character deep into the line is a space?

Solution

I solved a more general case. Consider a line where each word has a 50-50 chance of being $m$ or $n$ letters long, and each word is separated by exactly one space. In a line with many, many, many words, we can expect half the words to be $m$ letters long and half the words to be $n$ letters long.

It would be expected to have 2 spaces for every $m+n$ letters. The probability than any character is a space is :

$$\boxed{\frac{2}{m+n+2}}$$

Answer

For $m=3$ and $n=4$,

$$\boxed{\frac{2}{9}}$$

Extra Credit

Now let’s look for some rivers of text!

Fiddlish is written using a monospace font, meaning each character (including spaces) takes up the same amount of horizontal space. As before, lines of text are very, very long, and each next word has a 50 percent chance of being three letters and a 50 percent chance of being four letters. Each line begins with a new word (i.e., words at the end of a line are not hyphenated into the next line).

Suppose the 12th character of a specific line of text is a space. You want to know how long the river down and to the right from this space will be. For example, suppose the 13th character on the next line and the 14th character on the line after that are both spaces, but the 15th character on the very next line is not a space. In this case, the river would have a length of 3. (By this definition, the length of the river is always at least 1.)

On average, how long do you expect the resulting river from the given space (again, the 12th character in its line) to be?

Solution

The last character that is guaranteed to never be a space can also be solved generally. This aspect of the problem is identical to the Postage Stamp Problem or Chicken McNugget Problem.

Including the spaces, the $GCF(m+1, n+1) = 1$.

Evaluating $(m+1)(n+1) - (m+1) - (n+1) = mn-1$ for $m=3$ and $n=4$ yields $\boxed{11}$.

It is now known the given line with 12th character space is must be the start of the river.

I created code that did the following:

1. Initialize a dictionary representing the probability of a character being a space.
   • The 1^st, 2^nd, 3^rd, 6^th, 7^th, and 11^th characters are 0, as they are guaranteed to be letters.
   • The 4^th and 5^th characters each have a probability of $\frac{1}{2}$ to be a space.
2. Populate dictionary.
   • For index from 4 to 500, check if the probability of it being a space is $p = 0$.
     • If $p = 0$, that index has a letter, and cannot predict a future space.
     • If $p \neq 0$, that index has a space.
       • Increase the probability of index 4 characters away by $\frac{1}{2}p$.
       • Increase the probability of index 5 characters away by $\frac{1}{2}p$.
3. Initialize expected length $EL = 0$.
4. Initialize probability $P = 1$.
5. For index from $12 \le i \le 500$, check if the probability of it being a space is $p = 0$.
   • Initialize length $L = i-11$, as the river starts on character 12.
   • Set next $N$ as the probability the next character ($i+1$) is a space
   • Set $EL = L*P*(1-N)$.
   • Update $P$ by multiplying it by $N$.

Answer

$$\boxed{P \approx 1.5347081153095186}$$

The convergence is apparent very quickly...

Rohan Lewis

2025.05.26

Code can be found here.