Can You See Between the Trees?

Fiddler

This week, we’ll be returning to the forest with trees at integer coordinates.

You are at the point (0, 0) on the coordinate plane. There is a tree at each point with nonnegative integer coordinates, such as (5, 6), (0, 7), and (9, 1). The trees are very thin, so that they only obstruct trees that are directly behind them. For example, the tree at (2, 2) is not visible, as it is obscured by the tree at (1, 1).

Now, you can’t see infinitely far in this forest. Suppose, for example, that the farthest you can see is 4 units. The diagram below shows the trees you would see and the angles between them:

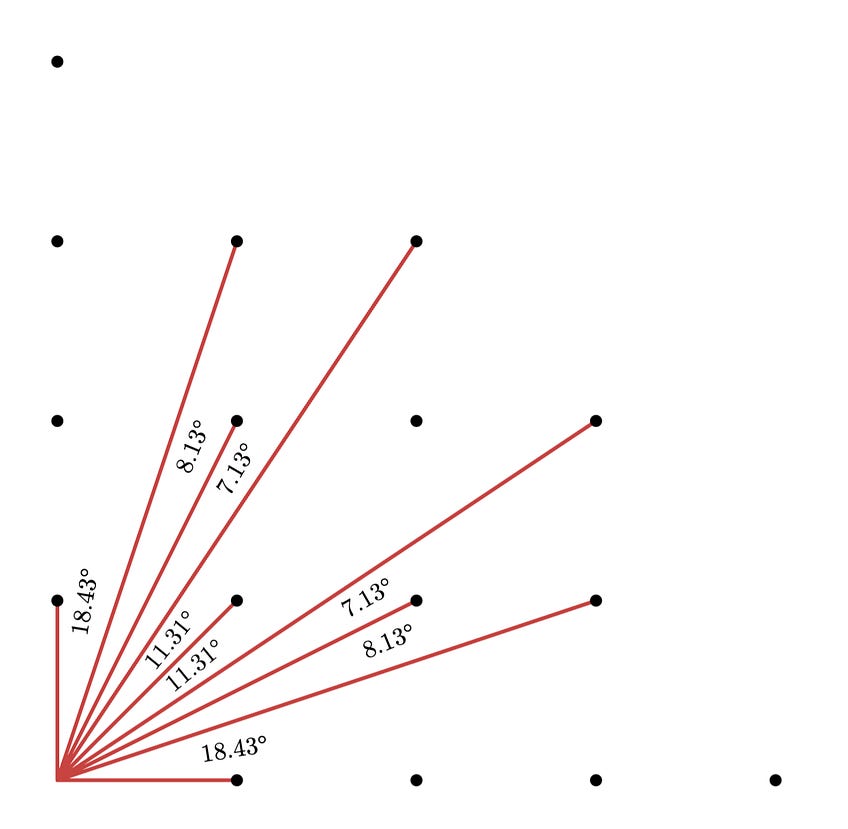
In truth, you can see much farther than 4 units into the forest. You’re not sure exactly how far you can see, but it’s pretty dang far. To be extra clear about this, the diagram above is just an illustration, and you can in fact see much farther than 4 units.

As you look around, you can make out very narrow angular gaps between the trees. The largest gaps are near the positive x-axis and the positive y-axis (similar to the illustrated case above). After those, the next largest pair of gaps are on either side of the tree at (1, 1), 45 degrees up from the x-axis.

Consider the view between 0 and 45 degrees up from the x-axis. The next largest pair of adjacent gaps in this range are on either side of what angle up from the x-axis? (To be clear, you are not considering the gap just above 0 degrees or the gap just below 45 degrees.)

Solution

I hypothesize that the order of the trees is identical to the order of their distance from you at $(0,0)$.

I wrote code that looked at a radius, ordered the trees by their angle, determined the difference in angle, and ordered by the difference.

In order to guarantee largest pair, there needs to be a minimum radius.

The following table summarizes my findings.

Pair	Tree Coordinates	Distance	Minimum Radius
$-$	$(1,0)$	$1.000$	1
$-$	$(1,1)$	$1.414$	2
$1$	$(2,1)$	$2.236$	8
$2$	$(3,1)$	$3.162$	21
$3$	$(3,2)$	$3.606$	22
$4$	$(4,1)$	$4.123$	22
$5$	$(4,3)$	$5.000$	195
$6$	$(5,1)$	$5.099$	195

Answer

$$\boxed{\tan^{-1}\frac{1}{2} \approx 26.5651^\circ}$$

Extra Credit

This week’s Fiddler asked to find the largest pair of adjacent gaps between 0 and 45 degrees.

The fifth largest pair of adjacent gaps in this range are on either side of what angle up from the x-axis? (Again, you are not considering the gap just above 0 degrees or the gap just below 45 degrees.)

Solution

Same as above...

Answer

$$\boxed{\tan^{-1}\frac{3}{4} \approx 36.8699^\circ}$$

Rohan Lewis

2025.04.28

Code can be found here.