A Pi Day Puzzle

Fiddler

From Jason Zimba (a colleague of mine at Amplify), comes a puzzle that’s perfect for Pi Day:

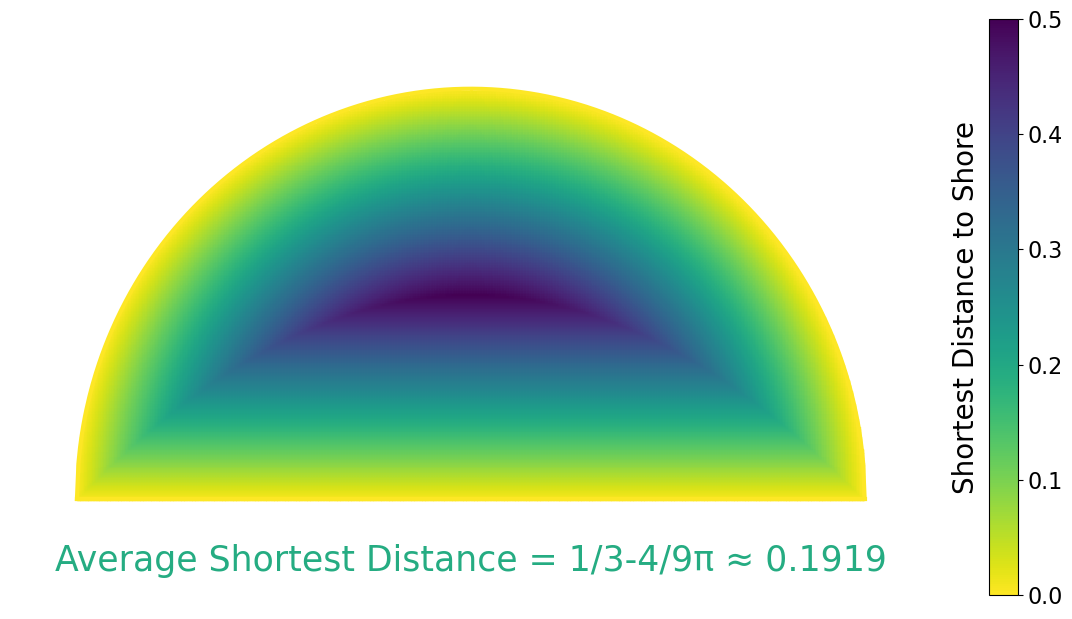
You are planning a picnic on the remote tropical island of 𝜋-land. The island’s shape is a perfect semi-disk with two beaches, as illustrated below: Semicircular Beach (along the northern semicircular edge of the disk) and Diametric Beach (along the southern diameter of the disk).

If you pick a random spot on 𝜋-land for your picnic, what is the probability that it will be closer to Diametric Beach than to Semicircular Beach? (Unlike the illustrative diagram above, assume the beaches have zero width.)

Solution

The shortest distance to Diametric Beach will always be along a path due south. The shortest distance to Semicircular Beach will always be a path along the radius of 𝜋-land.

Place the center of Diametric Beach at $(0,0)$ on a Cartesian Plane.

Equality occurs at :

\begin{align*} y &= 1 - \sqrt{x^2+y^2} \\ y^2 -2y + 1 &= x^2+y^2 \\ y &= \boxed{-\frac{x^2}{2} + \frac{1}{2}} \\ \end{align*}

The probabilty that the random spot will be closer to Diametric Beach than to Semicircular Beach is the area between the above equation and the x-axis divided by the area of 𝜋-land $\left(\frac{\pi}{2}\right)$.

Utilizing symmetry,

\begin{align*} A &= 2 \cdot \int\limits_0^1 \left(-\frac{x^2}{2} + \frac{1}{2}\right) dx \\ &= 2 \cdot \left[-\frac{x^3}{6} + \frac{x}{2} \right]_0^1 \\ &= 2 \cdot \left[\left(-\frac{1}{6}+\frac{1}{2}\right) - \left(-\frac{0}{6}+\frac{0}{2}\right) \right] \\ &= \boxed{\frac{2}{3}} \\ \end{align*}

Answer

The probability is thus,

$$P = \frac{\frac{2}{3}}{\frac{\pi}{2}} = \boxed{\frac{4}{3\pi} \approx 0.4244}$$

Extra Credit

From Jason Zimba also comes some Extra Credit:

Suppose the island of 𝜋-land, as described above, has a radius of 1 mile. That is, Diametric Beach has a length of 2 miles.

Again, you are picking a random point on the island for a picnic. On average, what will be the expected shortest distance to shore?

Solution

Converting to polar coordinates,

Additionally,

\begin{align*} y &= 1 - \sqrt{x^2+y^2} \\ r\sin\theta &= 1-r \\ r(\sin\theta +1) &= r \\ r &= \boxed{\frac{1}{\sin\theta +1}} \\ \end{align*}

$D(r, \theta)$, the shortest distance, can be expressed as:
$$D(r, \theta) = \Bigg[ \begin{array}{ll} r\sin\theta & 0\leq r\leq \frac{1}{sin\theta+1} \\ 1-r & \frac{1}{sin\theta+1} \leq r\leq 1 \\ \end{array} \Bigg]$$

Taking the double integral and divide by area to determine average shortest distance:

\begin{align*} A &= \frac{2 \cdot \int\limits_0^\frac{\pi}{2} \int\limits_0^1 D(r,\theta)\cdot r dr d\theta}{\frac{\pi}{2}}\\ &= \frac{4}{\pi} \cdot \int\limits_0^\frac{\pi}{2} \left(\int\limits_0^\frac{1}{\sin\theta+1} r\sin\theta\cdot r dr + \int\limits_\frac{1}{sin\theta+1}^1 (1-r)r dr\right) d\theta \\ &= \frac{4}{\pi} \cdot\int\limits_0^\frac{\pi}{2} \left(\int\limits_0^\frac{1}{\sin\theta+1} r^2\sin\theta dr + \int\limits_\frac{1}{sin\theta+1}^1 (r-r^2) dr\right) d\theta \\ &= \frac{4}{\pi} \cdot\int\limits_0^\frac{\pi}{2} \left(\left[\frac{r^3\sin\theta}{3} \right]_0^\frac{1}{\sin\theta+1} + \left[\frac{r^2}{2}-\frac{r^3}{3} \right]_\frac{1}{\sin\theta+1}^1 \right) d\theta \\ &= \frac{4}{\pi} \cdot\int\limits_0^\frac{\pi}{2} \Bigg(\left(\frac{\sin\theta}{3(\sin\theta+1)^3} - 0\right) + \left(\left(\frac{1}{2} - \frac{1}{3}\right) - \left(\frac{1}{2(\sin\theta+1)^2}-\frac{1}{3(\sin\theta+1)^3} \right)\right)\Bigg) d\theta \\ &= \frac{4}{\pi} \cdot \frac{1}{6} \cdot\int\limits_0^\frac{\pi}{2} \Bigg(1 + \frac{2\sin\theta - 3(\sin\theta+1) + 2}{(\sin\theta+1)^3}\Bigg) d\theta \\ &= \frac{2}{3\pi} \cdot \int\limits_0^\frac{\pi}{2} \Bigg(1 - \frac{\sin\theta + 1}{(\sin\theta+1)^3}\Bigg) d\theta \\ &= \frac{2}{3\pi} \cdot \int\limits_0^\frac{\pi}{2} \Bigg(1 - \frac{1}{(\sin\theta+1)^2}\Bigg) d\theta \\ \end{align*}

Answer

Using an integral solver,

$$\frac{2}{3\pi}\cdot\frac{3\pi-4}{6} = \boxed{\frac{1}{3}-\frac{4}{9\pi} \approx 0.1919}$$

I couldn't pass up on this heatmap...

Rohan Lewis

2025.03.17

Code can be found here.