Can You Break the Bell Curve?

Fiddler

Bean machines can famously produce bell-shaped curves. But today, we’re going to change all that!

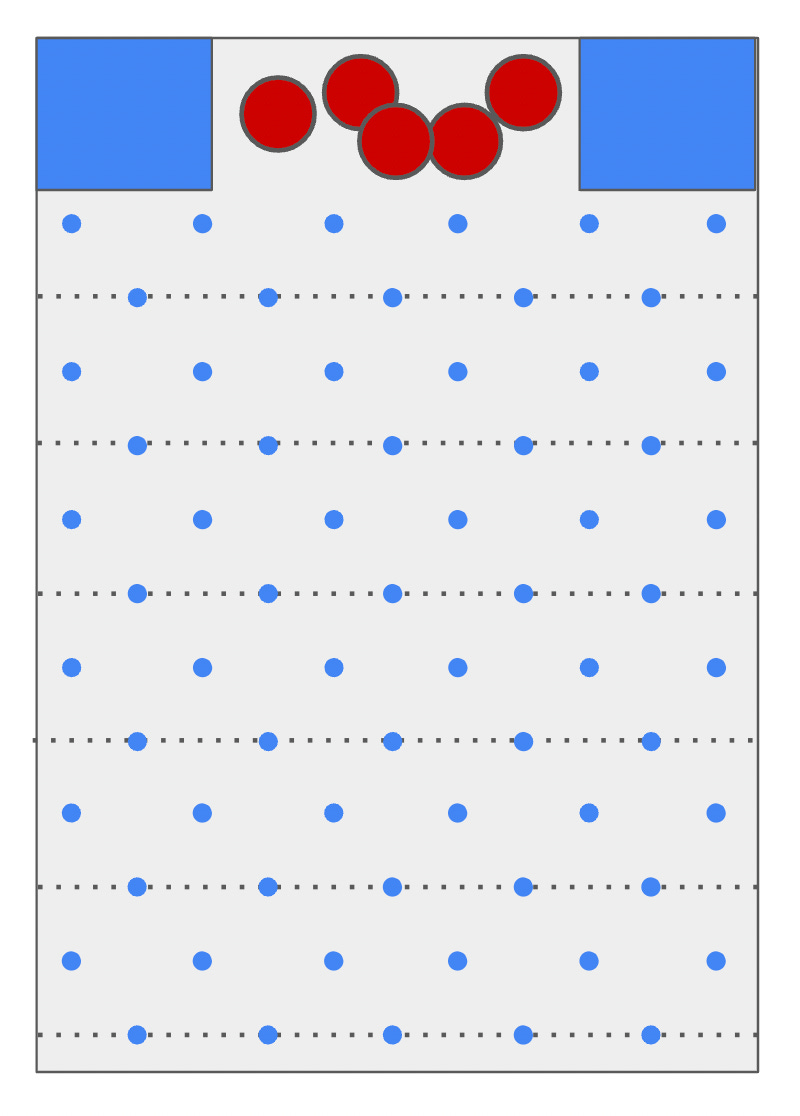
Suppose you have a board like the one shown below. The board’s topmost row has three pins (and two slots for a ball to pass through), while the bottommost row has two pins (and three slots for a ball to pass through). The remaining rows alternate between having three pins and two pins.

But instead of the 12 rows of pins in the illustrative diagram, suppose the board has many, many rows. And at the very bottom of the board, just below the two bottommost pins, are three buckets, labeled A, B, and C from left to right.

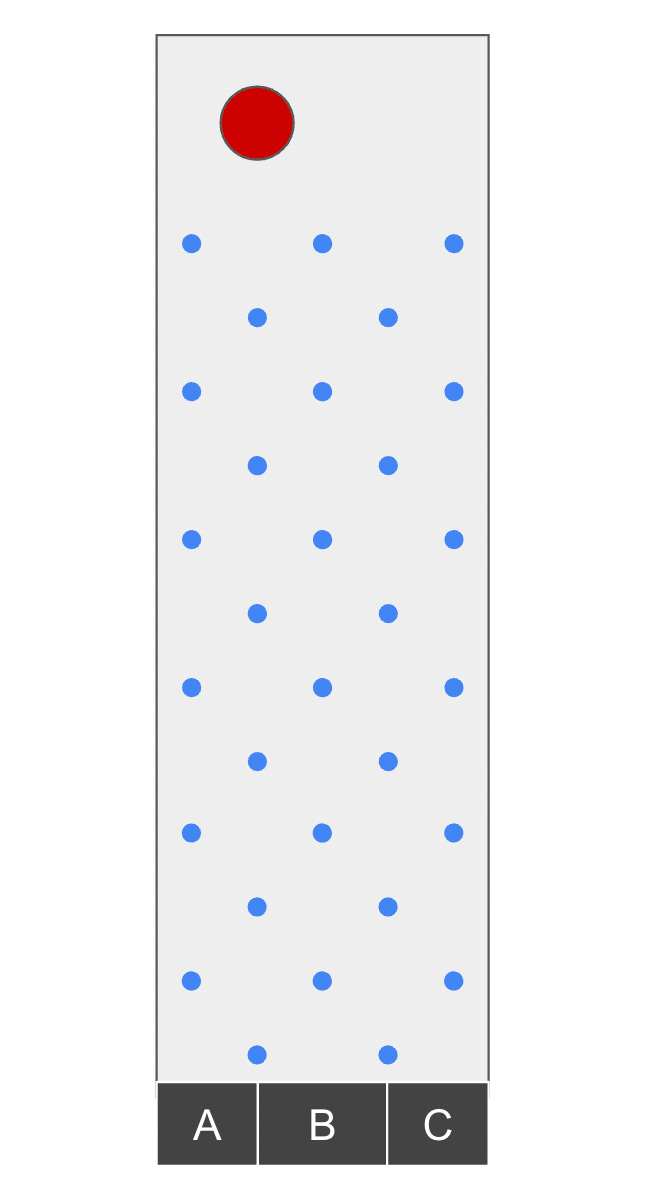
Whenever a ball encounters one of the leftmost pins, it travels down the right side of it to the next row. And whenever a ball encounters one of the rightmost pins, it travels down the left side of it to the next row.

But this isn’t your garden variety bean machine. Whenever a ball encounters any of the other pins, it has a 75 percent chance of traveling down the right side of that pin, and a 25 percent chance of traveling down the left side of that pin.

A single ball is about to be dropped into the left slot at the top of the board. What is the probability that the ball ultimately lands in bucket A, the leftmost slot at the bottom?

Solution

Consider the last three rows.

Let $P_a$, $P_b$, and $P_c$ denote the probability that the ball falls into bucket $A$, $B$, and $C$, respectively.

$P_l$ and $P_r$ are the left and right paths in the second-to-last row of pins.

$P_a$, $P_b$, and $P_c$ are also the probabilities of the three paths in the third-to-last row of pins.

The second-to-last row of pins yields:

\begin{align*} P_l = P_a + \frac{1}{4}P_b \\ P_r = \frac{3}{4}P_b + P_c \\ \end{align*}

The last row of pins yields :

\begin{align*} P_a &= \frac{1}{4}P_l \\ &= \frac{1}{4}\left(P_a + \frac{1}{4}P_b\right) \\ &= \frac{1}{4}P_a + \frac{1}{16}P_b \\ \frac{3}{4}P_a &= \frac{1}{16}P_b \\ P_a &= \boxed{\frac{1}{12}P_b} \\ \end{align*}\begin{align*} P_c &= \frac{3}{4}P_r \\ &= \frac{3}{4}\left(\frac{3}{4}P_b + P_c\right) \\ &= \frac{9}{16}P_b + \frac{3}{4}P_c \\ \frac{1}{4}P_c &= \frac{9}{16}P_b \\ P_c &= \boxed{\frac{9}{4}P_b} \\ \end{align*}

Solving,

\begin{align*} 1 &= P_a + P_b + P_c \\ &= P_b\left(\frac{1}{12} + 1 + \frac{9}{4}\right) \\ P_b &= \boxed{\frac{3}{10}}\\ \end{align*}

Answer

The probability that the ball ultimately lands in bucket A is:

$$P_a = \frac{1}{12}\times \frac{3}{10} = \boxed{\frac{1}{40}}$$

Extra Credit

Suppose you have the board below, which starts with a row with six pins (and five slots), followed by a row with five pins (and six slots), and then back to six pins in an alternating pattern. Balls are only allowed to enter through the middle three slots on top. This time around, the pins that aren’t on the far left or far right behave normally, meaning each ball is equally likely to go around it via the left side or the right side.

Your goal is to create a trapezoidal distribution along one of the rows with six slots, which have been highlighted with dotted lines in the diagram above. More precisely, the frequency of balls passing through the six slots from left to right should be x−y, x, x+y, x+y, x, x−y, for some values of x and y with x ≥ y.

Suppose the ratio by which you drop balls into the top three middle slots, from left to right, is a : b : c, with a + b + c = 1. Find all ordered triples (a, b, c) that result in a trapezoidal distribution in at least one row with six slots.

Solution

Given the symmetry of the distribution, $a = c$. Solving $a+b+c = 1 \rightarrow \boxed{b = -2a+1}$.

Given the symmetry of the distribution, $(x-y) + x + (x+y) = \frac{1}{2} \rightarrow \boxed{x = \frac{1}{6}}$.

Substiting and solving for the slots,

Row 2

$\frac{a}{2} = \frac{1}{6} \rightarrow a = \frac{1}{3}$.

$x = y = \frac{1}{6}$.

The distribution is $0, \frac{1}{6}, \frac{1}{3}, \frac{1}{3}, \frac{1}{6}, 0$.

$$(a,b,c) = \left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$$

.

Row 4

$\frac{a+1}{8} = \frac{1}{6} \rightarrow a = \frac{1}{3}$.

$x = \frac{1}{6}, y = \frac{1}{8}$.

The distribution is $\frac{1}{24}, \frac{1}{6}, \frac{7}{24}, \frac{7}{24}, \frac{1}{6}, \frac{1}{24}$.

$$(a,b,c) = \left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$$

.

Row 6

$\frac{2a+5}{32} = \frac{1}{6} \rightarrow a = \frac{1}{6}$.

$x = \frac{1}{6}, y = \frac{23}{192}$.

The distribution is $\frac{3}{64}, \frac{1}{6}, \frac{55}{192}, \frac{55}{192}, \frac{1}{6}, \frac{3}{64}$.

$$(a,b,c) = \left(\frac{1}{6}, \frac{2}{3}, \frac{1}{6}\right)$$

.

Rows 8, 10, and 12

From row 8, $\frac{22}{128} \gt \frac{1}{6}$. From row 10, $\frac{93}{512} \gt \frac{1}{6}$. From row 12, $\frac{385}{2048} \gt \frac{1}{6}$.

Since $a$ cannot be negative, no solutions are possible.

Answer

$$\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$$$$\left(\frac{1}{6}, \frac{2}{3}, \frac{1}{6}\right)$$

Rohan Lewis

2025.01.20

Code can be found here.