Can You Squeeze the Sheets?

Fiddler

From Q P Liu comes a bumpy way to start the new year:

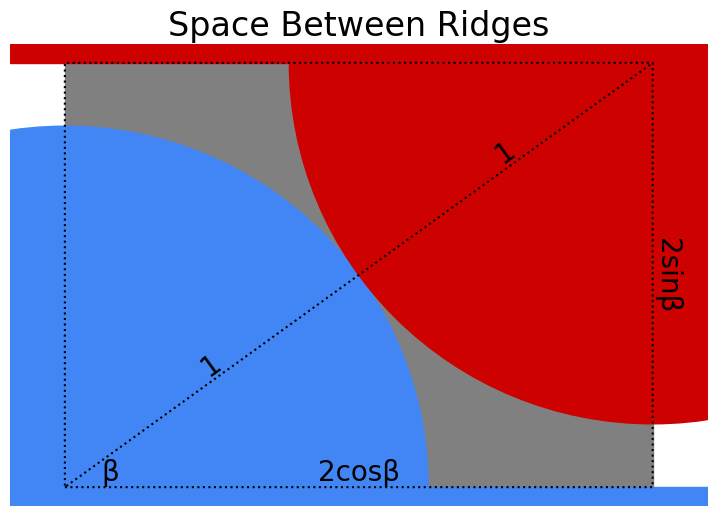
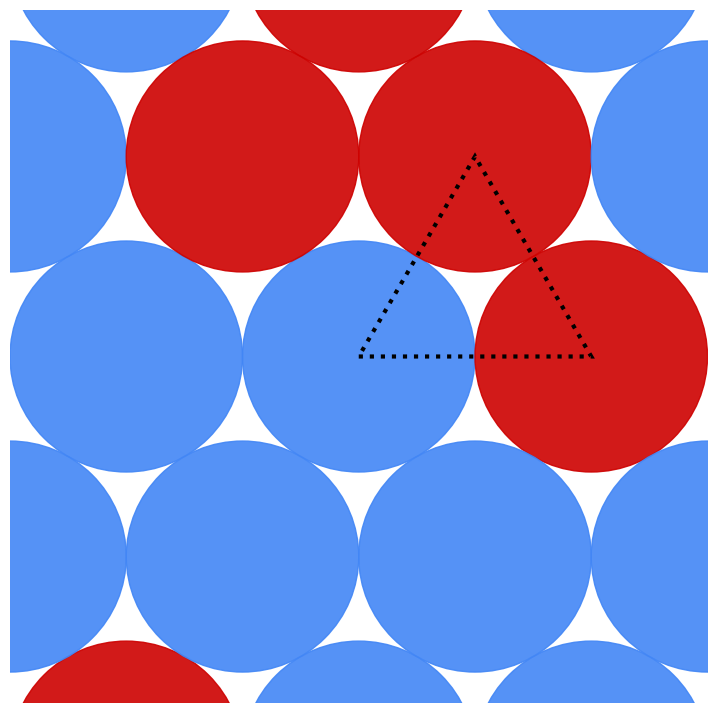
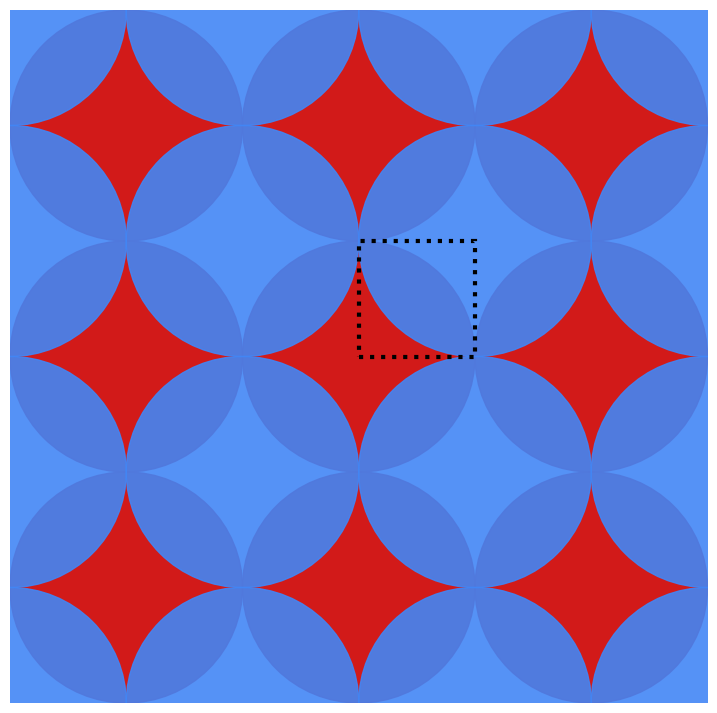
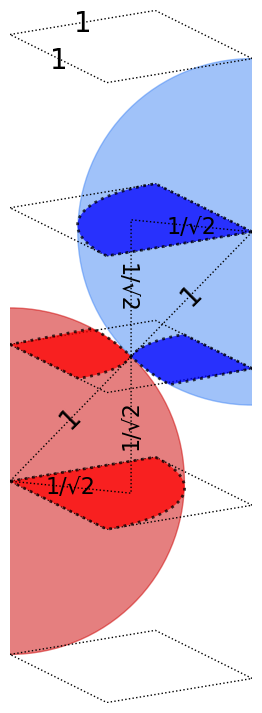
Two large planar sheets have parallel semicircular cylindrical ridges with radius 1. Neighboring ridges are separated by a distance L ≥ 2. The sheets are placed so that the ridges extrude toward each other, and so that the sheets cannot shift relative to each other in the horizontal direction, as shown in the cross-section below:

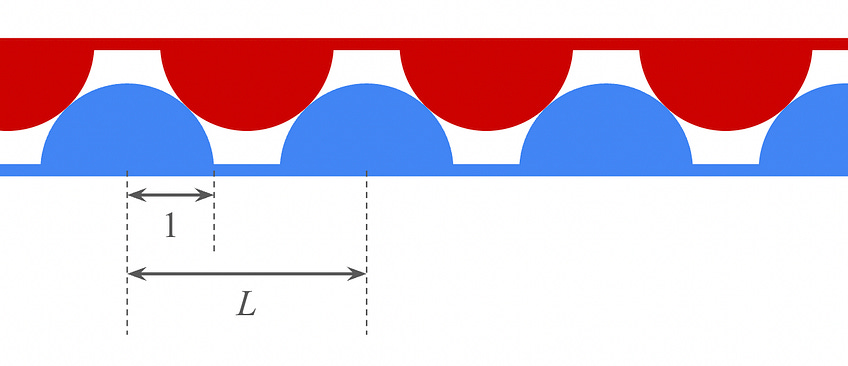
Which value of L (again, that’s the spacing between ridges) maximizes the empty space between the sheets?

To be clear, you are maximizing the volume of empty space per unit area of one flat sheet. In the cross-section shown above, that’s equivalent to maximizing the area of empty space per unit length of one flat sheet.

Solution

The section below repeats indefinitely throughout the two sheets.

The maximum ratio of empty space occurs when the grey area is maximized, as two quarter unit circles will always be subtracted from the area of the rectangles.

\begin{align*} A &= 2\cos\beta \cdot 2\sin\beta - 2\left(\frac{\pi}{4}\right) \\ A &= 2\sin (2\beta) - \frac{\pi}{2} \\ A' &= 4\cos (2\beta) = 0 \\ 0 &= \cos (2\beta) \\ \beta &= \boxed{\frac{\pi}{2}} \\ \end{align*}

The ratio is :

\begin{align*} R &= \frac{2-\frac{\pi}{2}}{2} \\ R &= \boxed{1-\frac{\pi}{4} \approx 0.2146} \\ \end{align*}

Answer

\begin{align*} L &= 4\cos\beta \\ L &= \boxed{2\sqrt{2}}\\ \end{align*}

Take a gander!

Extra Credit

From Q P Liu also comes some Extra Credit:

Instead of cylindrical ridges, now suppose the sheets have any number (greater than zero) of hemispherical deformations with radius 1 that extrude toward each other. This time, the sheets need not be the same as each other.

As before, the distance between the centers of any two deformations on the same sheet must be at least 2. What is the minimum empty space, again expressed as volume per unit area of one flat sheet?

Solution

I looked at two possibilities. The first was a hexagonal lattice of hemispheres. There is no pattern in either sheet, but both sheets must complement each other. Here is the top view:

The dotted triangle repeats indefinitely throughout the two sheets.

The triangle represents a triangular prism, with height $= 2$ and base side length $= 2$. The empty space is the remaining volume of the triangular prism after three $\frac{1}{6}$ spheres have been subtracted.

\begin{align*} V &= 2\cdot\frac{2^2\sqrt{3}}{4} - 3\cdot\frac{1}{6}\cdot\frac{4\pi}{3} \\ V &= 2\sqrt{3} - \frac{2\pi}{3} \\ R &= \boxed{\frac{2\sqrt{3} - \frac{2\pi}{3}}{2\sqrt{3}} \approx 0.3954}\\ \end{align*}

The second possibility are two sheets of hemispheres in a repeated square lattice. Any hemisphere of one sheet fits tangentially between four hemispheres of the other sheet.

The dotted square repeats indefinitely throughout the two sheets.

The square represents a rectangular prism, with unknown height and base side length $= 2$. The empty space is the remaining volume of the rectangular prism after two $\frac{1}{4}$ spheres have been subtracted.

It is clear that the height is $2+\sqrt{2}$.

\begin{align*} V &= 2+\sqrt{2} - 2\cdot\frac{1}{4}\cdot\frac{4\pi}{3} \\ V &= 2+\sqrt{2} - \frac{2\pi}{3} \\ R &= \boxed{\frac{2+\sqrt{2} - \frac{2\pi}{3}}{2+\sqrt{2}} \approx 0.3866}\\ \end{align*}

Answer

$$L = \boxed{2 \text{ or } 2\sqrt{2}}$$

Rohan Lewis

2025.01.06

Code can be found here.