Can You Survive "The Floor"?¶

Fiddler¶

From John Hannon comes a puzzle inspired by a television show:

In the game show, The Floor, 100 contestants are assigned to spaces on a 10×10 square grid. Over the course of a season, they compete one-on-one against their immediate neighbors by answering trivia questions. The loser of each duel is eliminated, and the square or squares they control are consigned to the winner.

Let’s consider a slightly simplified version of The Floor with nine contestants on a 3×3 square grid. Each round of the game consists of the following steps:

  • One of the remaining contestants is chosen at random. (Note that each contestant is equally likely to be chosen, regardless of how many squares they currently control.)

  • The set of eligible opponents for this contestant is anyone whose territory shares a common edge with the contestant. One of these eligible opponents is chosen at random. (Again, all eligible opponents are equally likely to be chosen, regardless of how many squares they control or how many edges they have in common with the opponent.)

  • The contestant and their selected opponent have a duel, each with a 50 percent chance of winning. The loser is eliminated, and their territory is added to that of the winner.

These rounds repeat until one contestant remains, and that contestant is the overall winner.

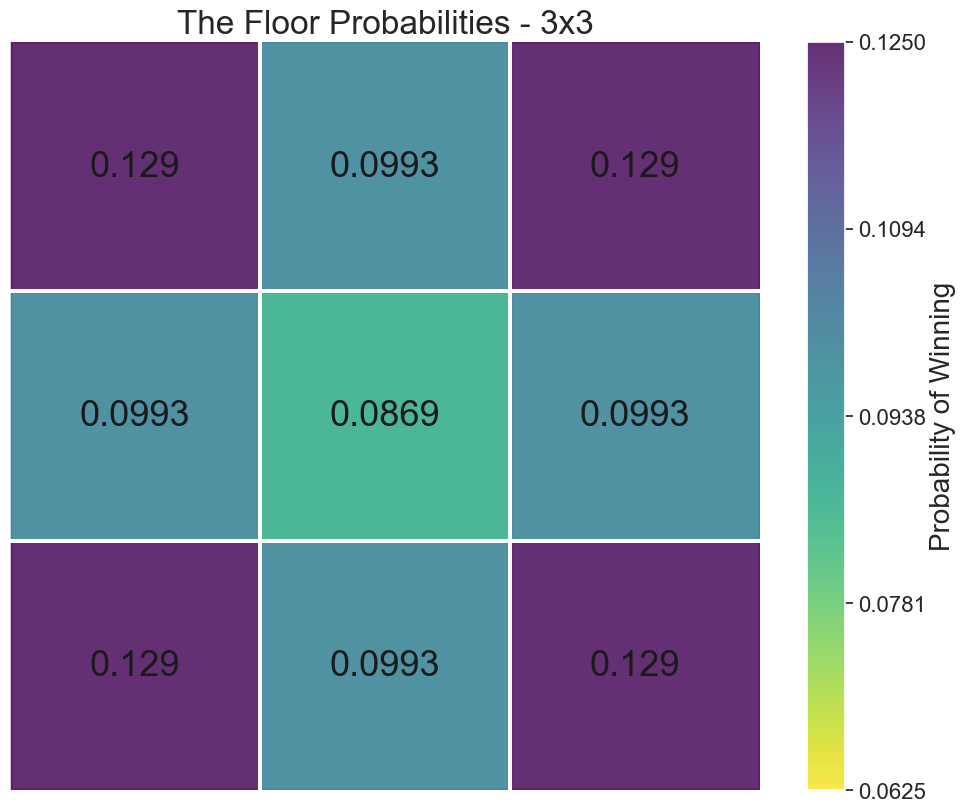
You are a contestant on a new season of this 3×3 version of The Floor. The nine positions on the grid are shown below:

Which position would you choose? That is, which position or positions give you the best chance of being the overall winner?

Solution¶

I created code that did the following :

  1. Start with :
    1. An dictionary of Territory ownership :
      1. Each key is a player denoted by $(x, y)$.
      2. Each value is a list of territories the player occupies.
      3. Each of the $N^2$ players initially occupies only the territory the same as their name.
    2. A dictionary of Common Edges :
      • For each player as a key:
        1. Look at the cells left of, above, right of, and below.
        2. If the neighbor exists and has not already been identified as a neighbor, add it to list of neighbors.
        3. Add the list as the value.
  2. While there are at least two players:
    1. Randomly select a player.
    2. Randomly select a neighbor.
    3. Randomly select a winner $P_j$ and loser $P_k$ from the two.
    4. Update the Territory :
      1. Append the $P_k$'s territory to that of $P_j$.
      2. Remove $P_k$.
    5. Update the Common Edges :
      1. For each non-$P_j$ neighbor of the $P_k$, replace $P_k$ with $P_j$.
      2. Append the $P_k$'s neighbors to that of $P_j$. Remove $P_k$ and $P_j$ from that list.
      3. Remove $P_k$.
    6. There is now one less player. Continue.
  3. Return the last remaining player.

Answer¶

I ran $1,000,000$ trials for a $3x3$ The Floor.

The 4 corners seem to have each a probability of $~0.1288$, which is significantly greater than $\frac{1}{9}$.

It makes sense that the corners have higher probabilities, as they have two directions from which they will never be attacked, no matter how large their territory gets.

Extra Credit¶

Again, a new season of the 3×3 version of The Floor (as described above) is about to begin.

What is your probability of winning for each of the nine starting positions?

Answer¶

The edges are significantly greater than the center, as they have one direction from which they will never be attacked.

Extra Extra Credit¶

And for Extra Extra Credit, suppose there are N2 positions on an N×N square grid. What is your probability of winning from each of these?

Solution¶

Just kidding, I ran $1,000,000$ trials for all The Floor scenarios for $N = 2$ to $25$. I also accounted for symmetry and averaged cells that can be transposed by rotation or reflection.

$N = 2$ is unique, as the four corners are also the four centers.

I noticed for $N>2$ the corner probabilities, or upper limit of win probability, is $\boxed{\frac{2}{(N+1)^2}}$.

The center probabilities, or lower limit for win probability, is $\boxed{\frac{1}{(N+1)^2}}$.

I couldn't explain this...so I animated it.

Rohan Lewis¶

2024.12.13¶

Code can be found here.