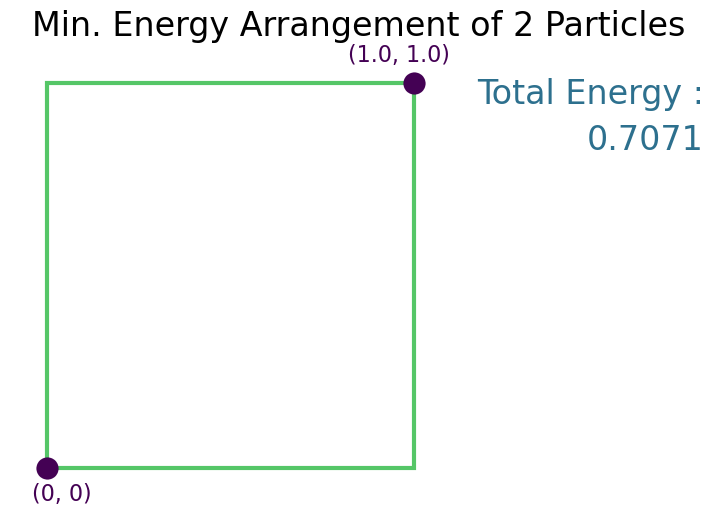
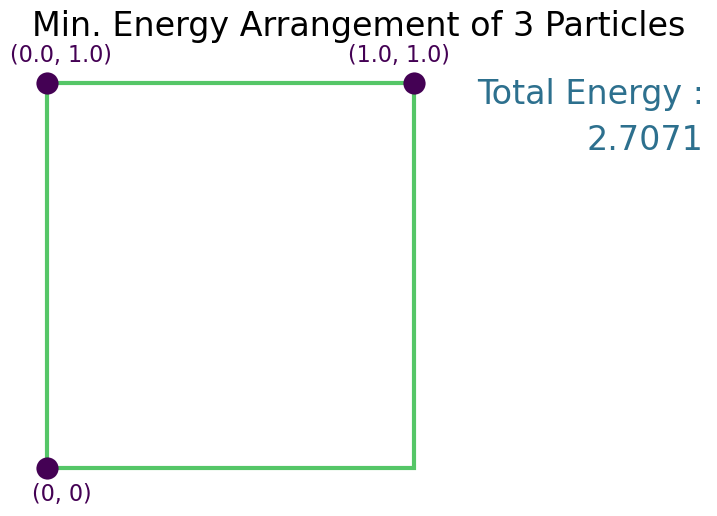
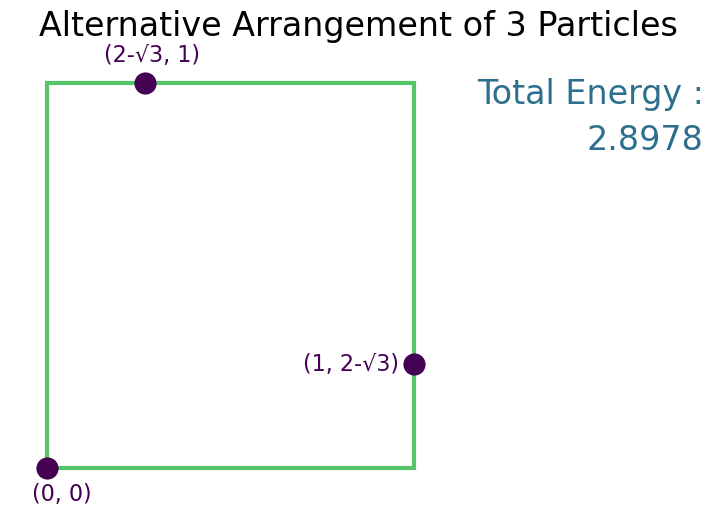
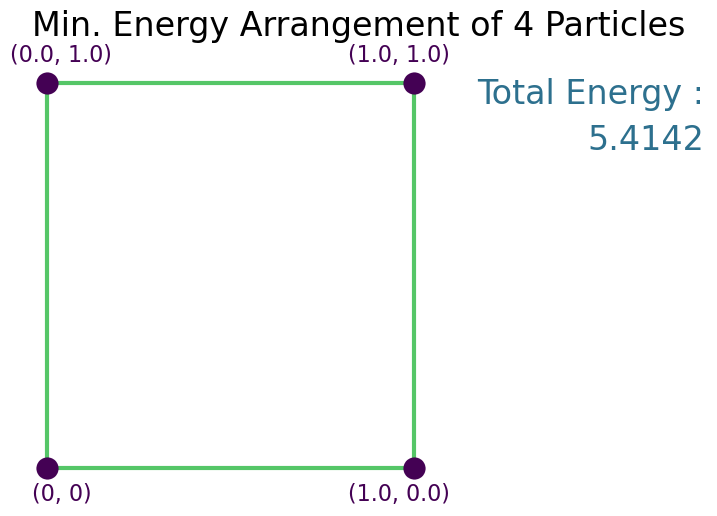
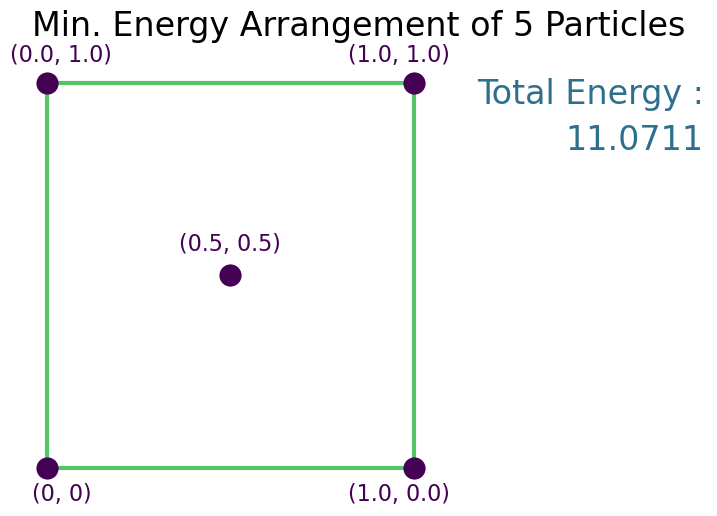
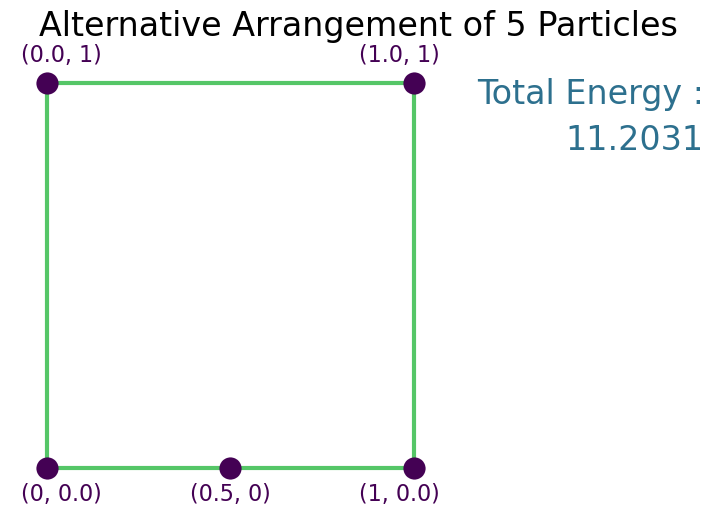
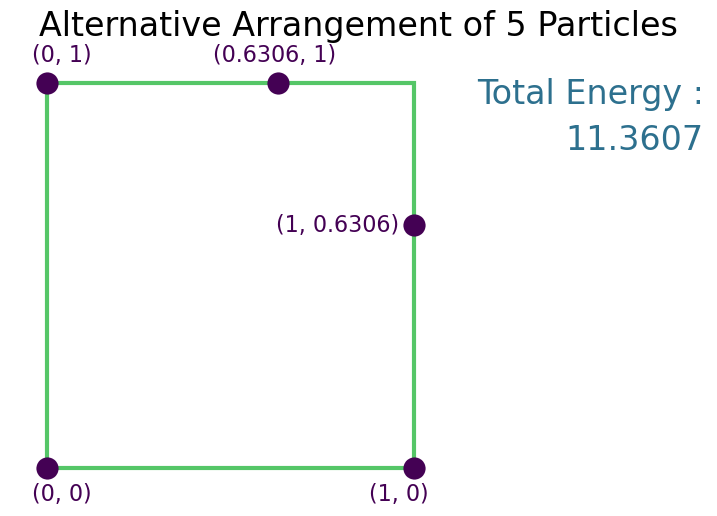
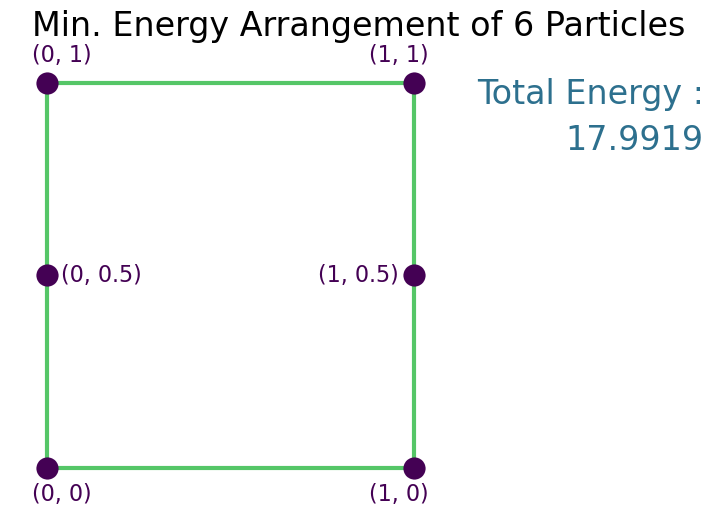
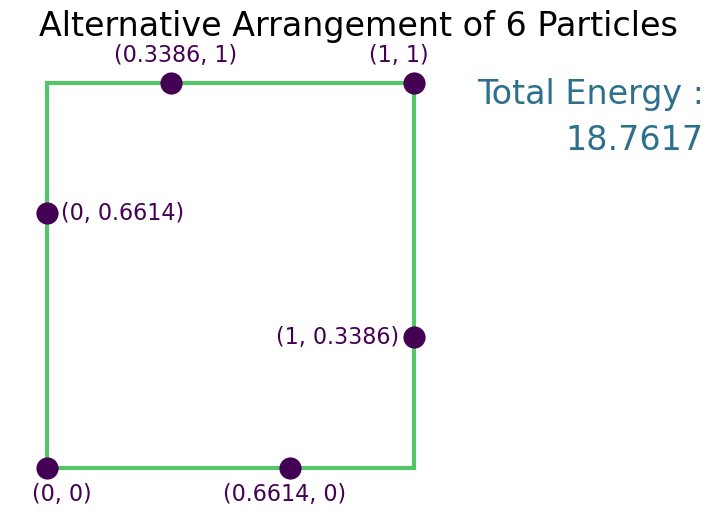
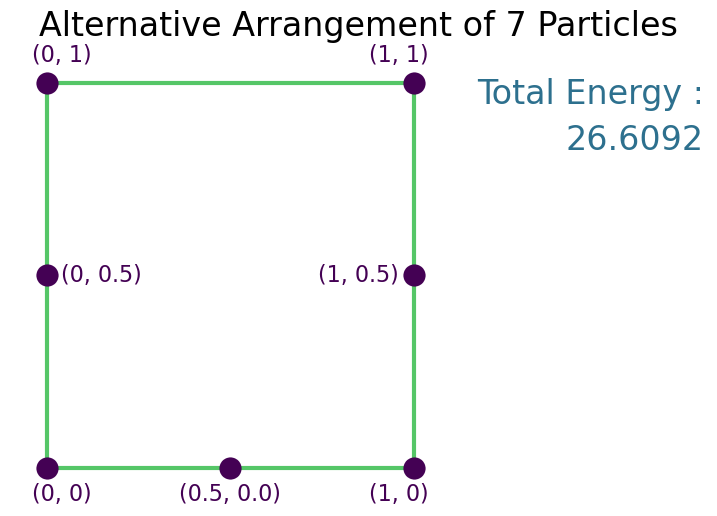
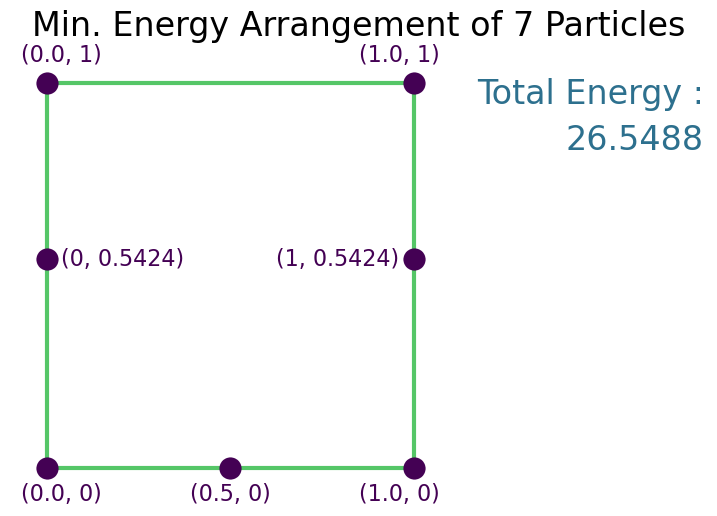
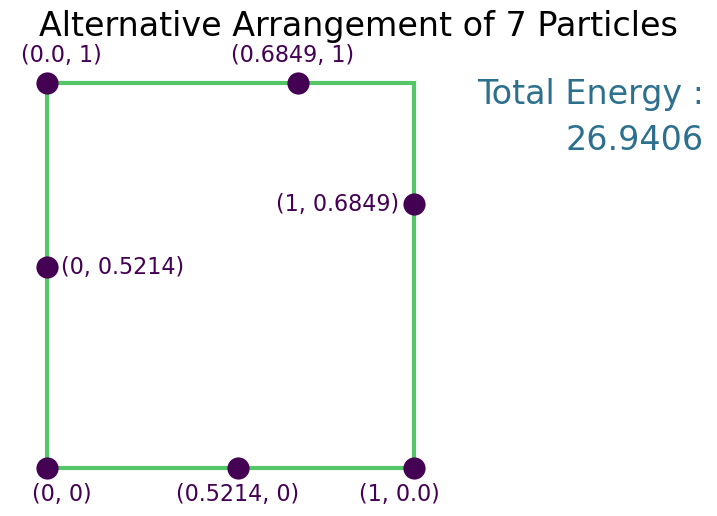
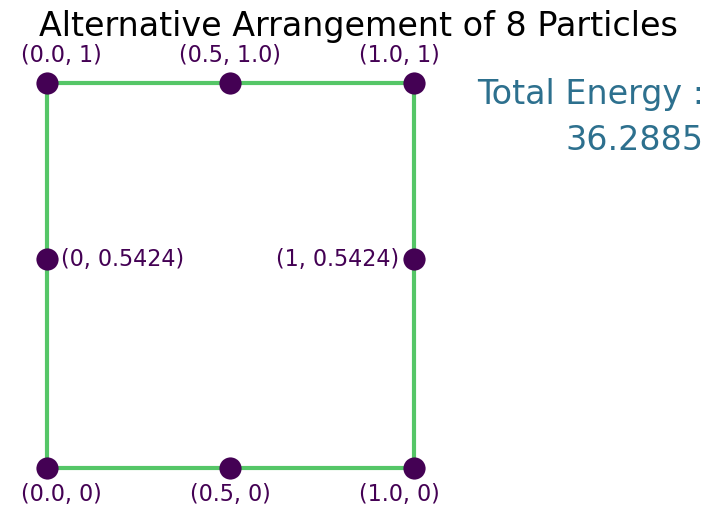
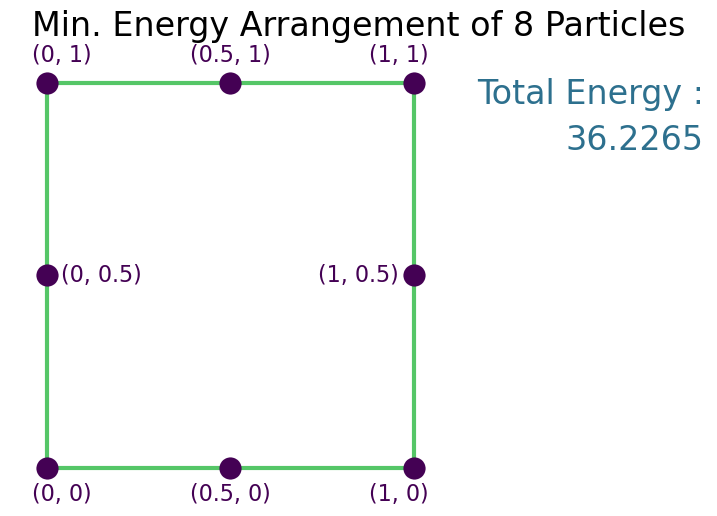
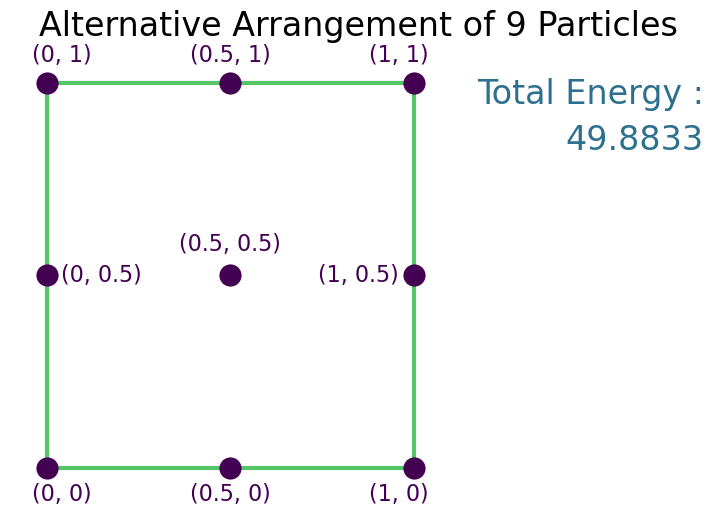
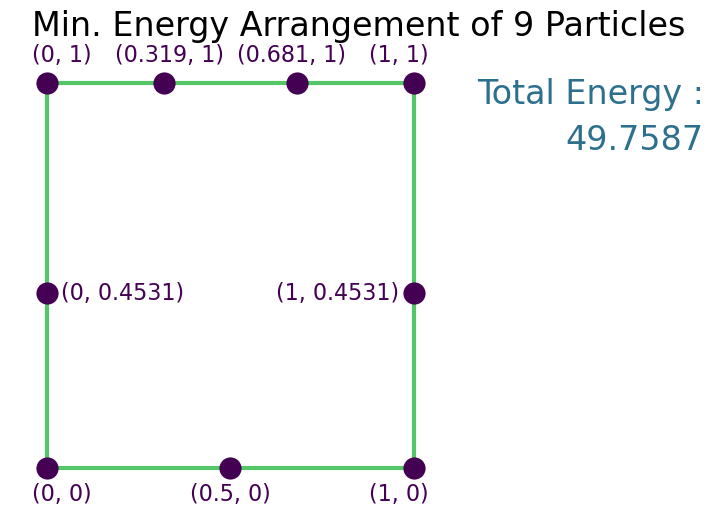
Solution¶
I first explored symmetry and minimizing energy.
When placing a third particle given two diametrically opposite particles, is the energy minimized by centering the third point or placing it $x$ off center? I did not find this to be obvious.
The sum of the energy is :
$$E(x) = \frac{1}{\sqrt{(a-x)^2+b^2}} + \frac{1}{\sqrt{(a+x)^2+b^2}}$$
The first derivative of the energy is
$$
\begin{align*}
E'(x) &= -\frac{1}{2}\frac{2(a-x)(-1)}{\left((a-x)^2+b^2\right)^{3/2}} -\frac{1}{2}\frac{2(a+x)}{\left((a+x)^2+b^2\right)^{3/2}} \\
&= \frac{a-x}{\left((a-x)^2+b^2\right)^{3/2}} - \frac{a+x}{\left((a+x)^2+b^2\right)^{3/2}} \\
\end{align*}
$$
$x = 0$ yields:
$$\frac{a}{\left(a^2+b^2\right)^{3/2}} - \frac{a}{\left(a^2+b^2\right)^{3/2}} = 0$$
Taking the second derivative of the first fraction of $E(x)$,
$$ \begin{align*} \frac{d\big[(a-x)\left((a-x)^2+b^2\right)^{-3/2}\big]}{dx} &= (a-x)\left((a-x)^2+b^2\right)^{-5/2}\cdot\left(\frac{-3}{2}\right)(2\cdot(a-x)\cdot-1) - \left((a-x)^2+b^2\right)^{-3/2} \\ &= \left((a-x)^2+b^2\right)^{-5/2}\left(3(a-x)^2 - ((a-x)^2+b^2)\right) \\ &= \frac{2(a-x)^2-b^2}{((a-x)^2+b^2)^{5/2}}\\ \end{align*} $$
Taking the second derivative of the second fraction of $E(x)$,
$$
\begin{align*}
\frac{d\big[(a+x)\left((a+x)^2+b^2\right)^{-3/2}\big]}{dx} &= (a+x)\left((a+x)^2+b^2\right)^{-5/2}\cdot\left(\frac{-3}{2}\right)(2\cdot(a+x)\cdot1) + \left((a+x)^2+b^2\right)^{-3/2} \\
&= \left((a-x)^2+b^2\right)^{-5/2}\left(-3(a+x)^2 + ((a+x)^2+b^2)\right) \\
&= \frac{-2(a+x)^2+b^2}{((a+x)^2+b^2)^{5/2}}\\
\end{align*}
$$
Thus,
$$
\begin{align*}
E"(x) &= \frac{2(a-x)^2-b^2}{((a-x)^2+b^2)^{5/2}} - \frac{-2(a+x)^2+b^2}{((a+x)^2+b^2)^{5/2}} \\
&= \frac{2(a-x)^2-b^2}{((a-x)^2+b^2)^{5/2}} + \frac{2(a+x)^2-b^2}{((a+x)^2+b^2)^{5/2}} \\
E"(0) &= \frac{2a^2-b^2}{(a^2+b^2)^{5/2}} + \frac{2a^2-b^2}{(a^2+b^2)^{5/2}} \\
&= \frac{4a^2-2b^2}{(a^2+b^2)^{5/2}} \\
\end{align*}
$$
Symmetry in this scenario yields minimum energy as long as $2a > b\sqrt{2}$. I shall keep this in mind...