Solution¶
From Rock, Paper, Scissors, Lizard, Spock is the following diagram.
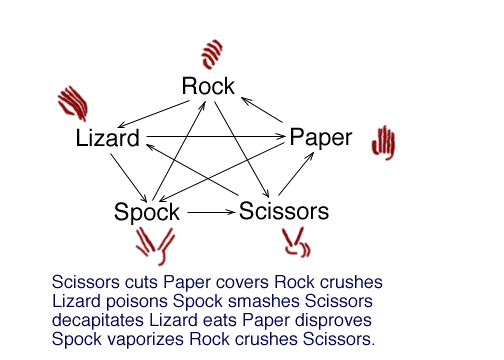
The problem is asking how many ways one can traverse through all 10 segments exactly once in order.
In a game of “Rock, Paper, Scissors,” each element you can throw ties itself, beats one of the other elements, and loses to the remaining element. In particular, Rock beats Scissors beats Paper beats Rock.
“Rock, Paper, Scissors, Lizard, Spock” (popularized via The Big Bang Theory) is similar, but has five elements you can throw instead of the typical three. Each element ties itself, beats another two, and loses to the remaining two. More specifically, Scissors beats Paper beats Rock beats Lizard beats Spock beats Scissors beats Lizard beats Paper beats Spock beats Rock beats Scissors.
Three players are playing “Rock, Paper, Scissors, Lizard, Spock.” At the same time, they all put out their hands, revealing one of the five elements. If they each chose their element randomly and independently, what is the probability that one player is immediately victorious, having defeated the other two?
There are $5^3 = 125$ outcomes. Here are the possibilities.
Every player plays the same hand.
$\dfrac{5 \cdot 1 \cdot 1}{125} = \boxed{\frac{5}{125}}$
Every player beats one player and loses to another. This creates a loop with no clear winner. There are 5 distinct antitransitive loops :
There are $3!$ the players can create each loop.
$\dfrac{5 \cdot 1 \cdot 1 \cdot 3!}{125} = \boxed{\frac{30}{125}}$
Two players choose exactly the same hand. The third player chooses one of the two hands that loses to that hand. There are $3 \choose 1$ ways to pick the loser.
$\dfrac{5 \cdot 1 \cdot 2 \cdot 3}{125} = \boxed{\frac{30}{125}}$
The winner can choose any hand. The two other players choose from the two hands that lose to that hand. There are three ways that can occur:
$\dfrac{(5 \cdot 1 \cdot 1 \cdot 6) + (5 \cdot 1 \cdot 1 \cdot 3) + (5 \cdot 1 \cdot 1 \cdot 3)}{125} = \boxed{\frac{60}{125}}$
The four cases sum to $1$. The answer is $\dfrac{(5 \cdot 1 \cdot 1 \cdot 6) + (5 \cdot 1 \cdot 1 \cdot 3) + (5 \cdot 1 \cdot 1 \cdot 3)}{125} = \boxed{\frac{60}{125}} = \boxed{0.48}$
The rules for “Rock, Paper, Scissors” can concisely be written in one of the following three ways:
Rock beats Scissors beats Paper beats Rock
Scissors beats Paper beats Rock beats Scissors
Paper beats Rock beats Scissors beats Paper
Each description of the rules includes four mentions of elements and three “beats.”
Meanwhile, as previously mentioned, a similarly concise version of the rules for “Rock, Paper, Scissors, Lizard, Spock” (and adapted from the original site) is:
Scissors beats Paper beats Rock beats Lizard beats Spock beats Scissors beats Lizard beats Paper beats Spock beats Rock beats Scissors
In this case, there are 11 mentions of elements and 10 “beats.” Including the one above, how many such ways are there to concisely describe the rules for “Rock, Paper, Scissors, Lizard, Spock?”
From Rock, Paper, Scissors, Lizard, Spock is the following diagram.

The problem is asking how many ways one can traverse through all 10 segments exactly once in order.