Can You Make a Toilet Paper Roll?

Fiddler

From one of my kids comes a question worth pondering … on the toilet:

Suppose you have the parallelogram of cardboard shown below, which has side lengths of 2 units and 6 units, and angles of 30 degrees and 150 degrees:

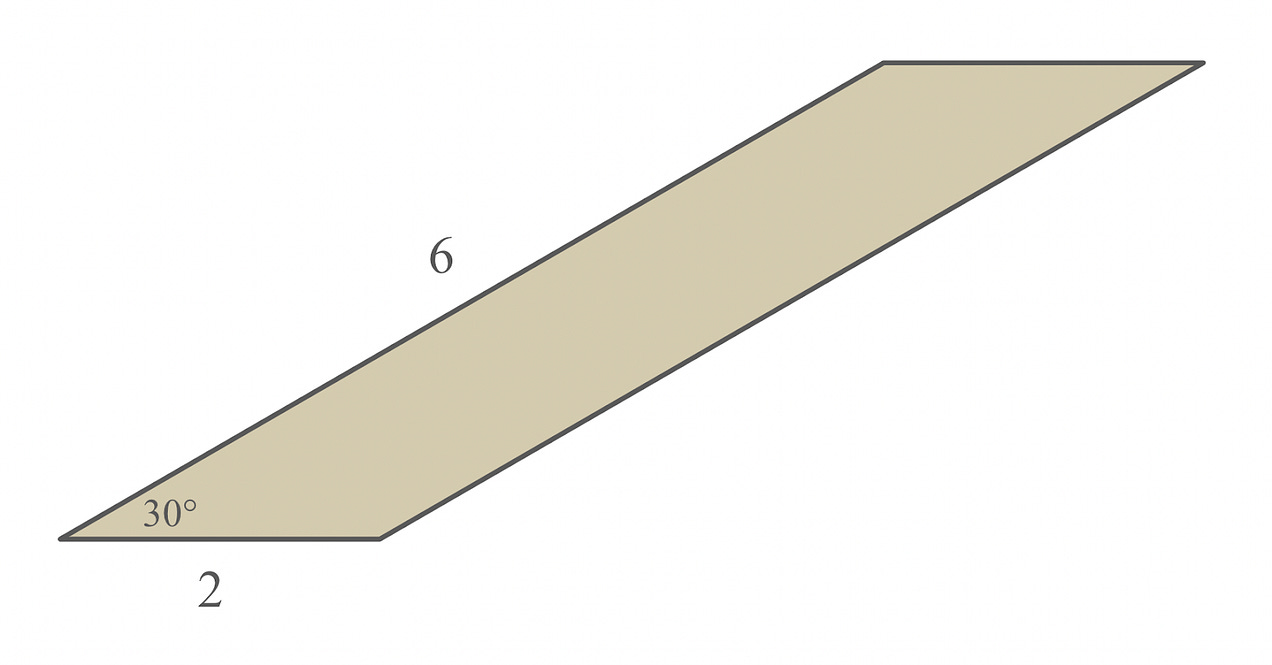
By swirling two edges together, it’s possible to neatly (without any overlap) generate the lateral surface of a right cylinder—in other words, a toilet paper roll! (If you’re not convinced, try gently tearing a toilet paper roll along its diagonal seam and then unwrapping it into a flat shape. You get a parallelogram!)

Determine the volume of a cylinder you can make from this particular piece of cardboard.

Solution

The area of a parallelogram is $$A = ab\sin \theta$$

There are two cylinders that can be generated.

Case I.

The height is $a\sin \theta$. The circumference is $b$, so the base area is $\dfrac{b^2}{4\pi}$.

\begin{align*} V &= a\sin \theta \cdot \dfrac{b^2}{4\pi} \\ &= 2\sin 30^{\circ} \cdot \dfrac{6^2}{4\pi} \\ &= 2\cdot\frac{1}{2} \cdot \dfrac{9}{\pi} = \boxed{\dfrac{9}{\pi}}\\ \end{align*}

Case II.

The height is $b\sin \theta$. The circumference is $a$, so the base area is $\dfrac{a^2}{4\pi}$.

\begin{align*} V &= b\sin \theta \cdot \dfrac{a^2}{4\pi} \\ &= 6\sin 30^{\circ} \cdot \dfrac{2^2}{4\pi} \\ &= 6\cdot\frac{1}{2} \cdot \dfrac{1}{\pi} = \boxed{\dfrac{3}{\pi}}\\ \end{align*}

Answer

$\boxed{\dfrac{9}{\pi}}$ and $\boxed{\dfrac{3}{\pi}}$.

Extra Credit

Suppose you have a parallelogram with an area of 1 square unit. Let V represent the average volume of all cylinders whose lateral surface you can neatly make by swirling two edges of the parallelogram together.

What is the minimum possible value of V?

Solution

From above,

\begin{align*} V &= \frac{\left(a\sin \theta \cdot \dfrac{b^2}{4\pi}\right) + \left(b\sin \theta \cdot \dfrac{a^2}{4\pi}\right)}{2} \\ &= \frac{ab\sin\theta}{4\pi} \cdot \frac{a+b}{2} \end{align*}

Substituting $1 = ab\sin\theta$ yields $V = \dfrac{a+b}{8\pi}$.

Minimizing $V$ means minimimizing $a$ and $b$, which means maximizing $\sin\theta$.

$\theta = 90^\circ$, $a = b = 1$, and the parallelogram is a unit square.

Answer

$$\boxed{V = \frac{1}{4\pi}}$$

Rohan Lewis

2024.09.23