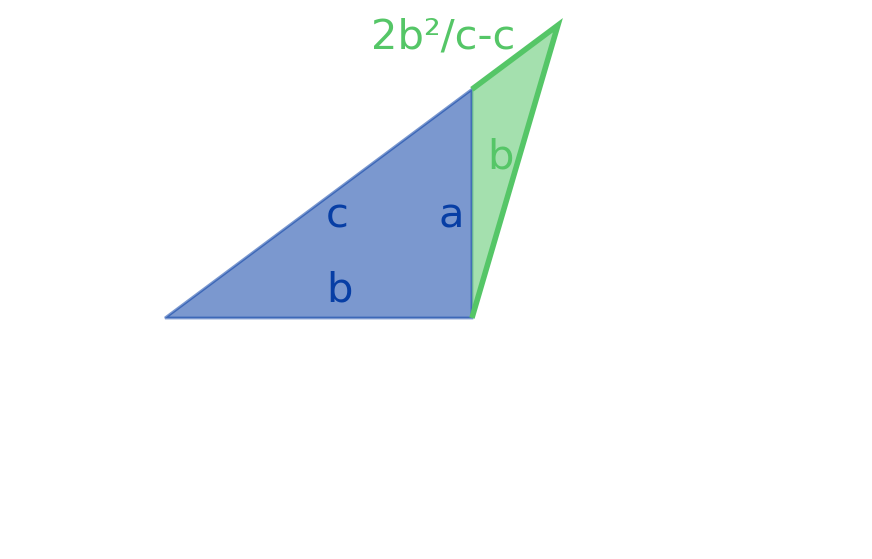
Can You Turn a Right Triangle Into an Isosceles Triangle?

Fiddler

From Dean Ballard and his daughter comes a puzzle they recalled from “the Greater Internet Hivemind”:

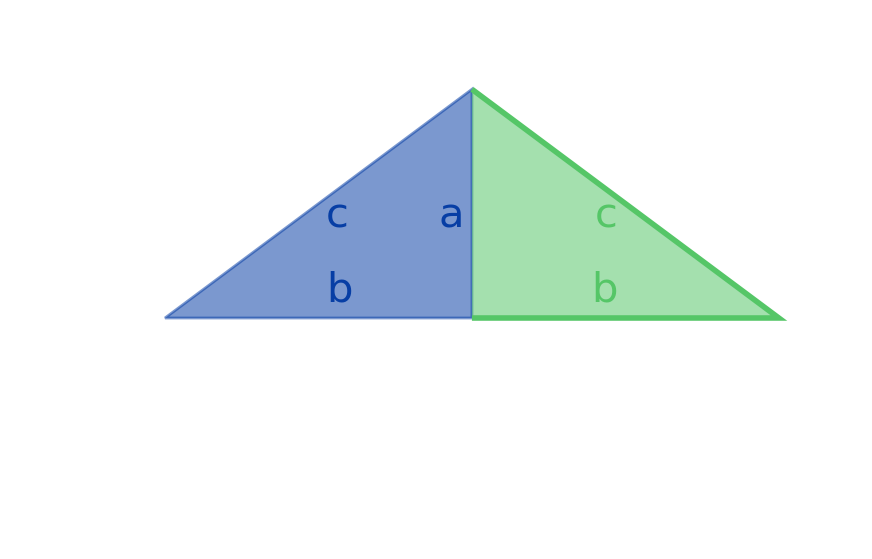
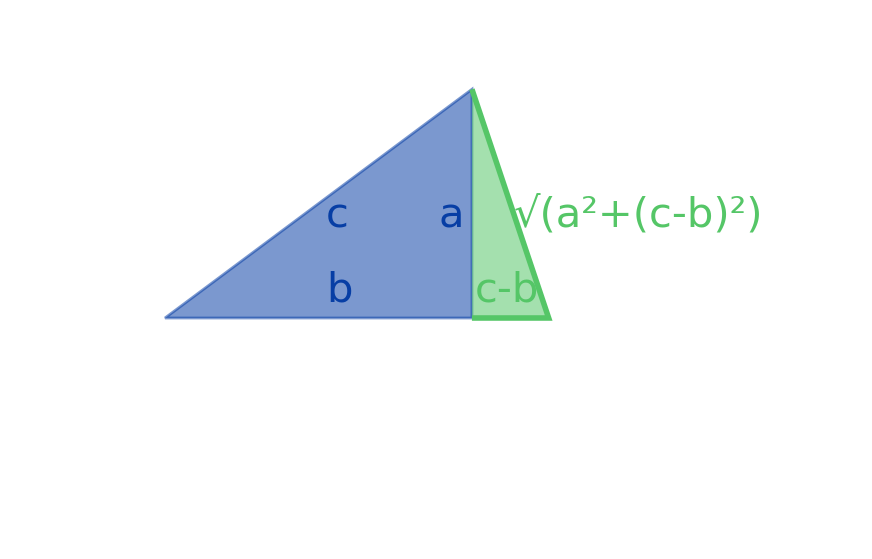
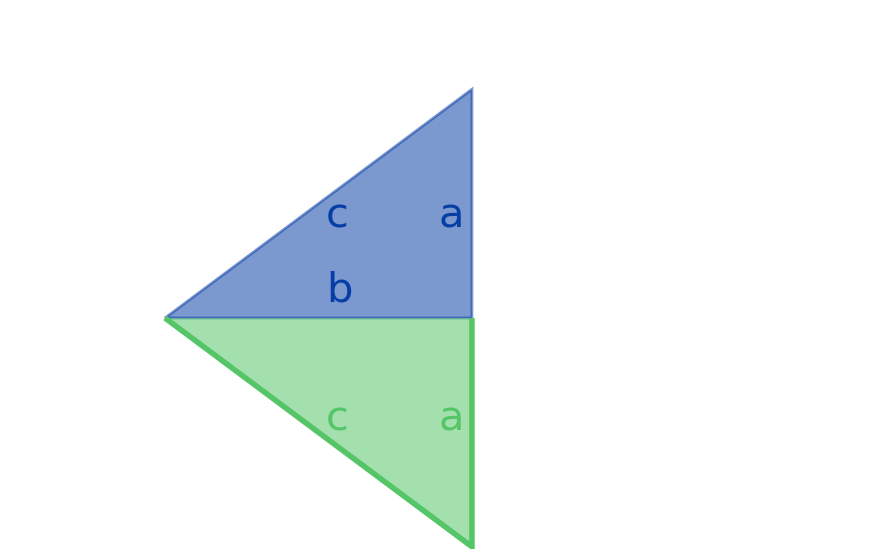
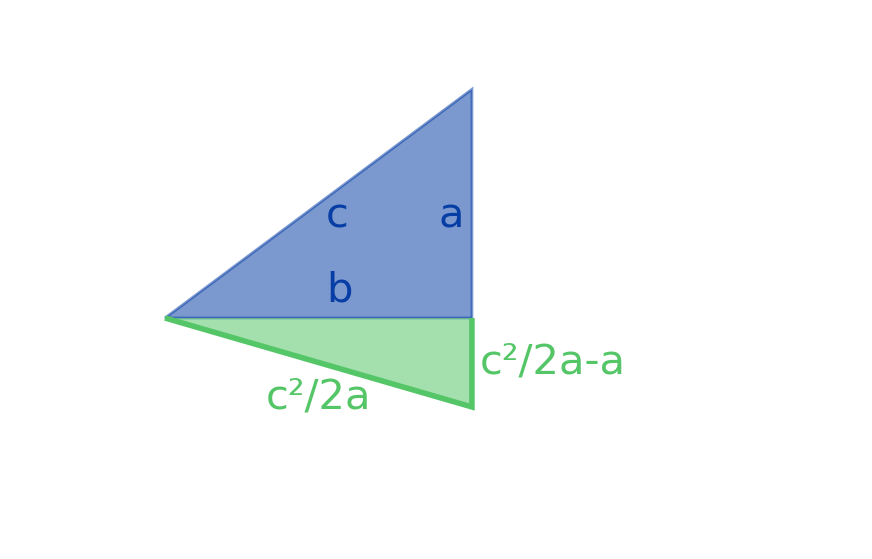
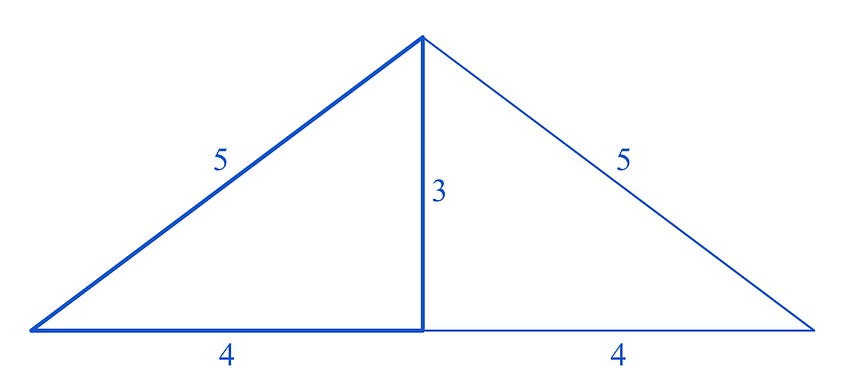
Beginning with a 3-4-5 right triangle, it’s possible to append another triangle to one of its sides, thereby making an isosceles triangle. For example, here is how you can make a 5-5-8 isosceles triangle:

Including the one given above, how many distinct ways can you append a triangle to a 3-4-5 right triangle to make an isosceles triangle?

Solution

WLOG, $a \le b < c$. Exactly one side of the original triangle will be identical in the new isosceles triangle, and it is impossible for that side to be $a$.

The cases that follow are defined by the resulting isosceles triangle.

Case I. $c-c-x$

There are four ways this can occur.

1. $c-c-2b$

Flip the triangle along its short leg.

2. $c-c-\sqrt{a^2+(c-b)^2)}$

Extend the long leg until it is the length of the hypotenuse.

3. $c-c-2a$

Flip the triangle along its long leg.

4. $c-c-\sqrt{b^2+(c-a)^2)}$

Extend the short leg until it is the length of the hypotenuse.

Case II. $c-y-y$

There is one way this can occur.

$c-\dfrac{c^2}{2a}-\dfrac{c^2}{2a}$

Extend the short leg until it is the length of the new non-$c$ side. The value is $\dfrac{c^2}{2a}$ because of similar triangles.

Case III. $b-b-z$

There are two ways this can occur.

1. $b-b-b\sqrt{2}$

Extend the short leg until it is the length of the long leg.

2. $b-b-\dfrac{2b^2}{c^2}$

Extend the hypotenuse until the third side is the length of the long leg. The value is $\dfrac{2b^2}{c}$ because of similar triangles.

Answers

For a $3-4-5$ triangle this results in the following isosceles triangles:

• $5-5-8$
• $5-5-\sqrt{10}$
• $5-5-6$
• $5-5-2\sqrt{5}$
• $5-\dfrac{25}{6}-\dfrac{25}{6}$
• $4-4-4\sqrt{2}$
• $4-4-\dfrac{32}{5}$

Extra Credit

Now suppose you have a right triangle with legs of length a and b and a hypotenuse of length c. And suppose further that there are N distinct ways to append a triangle to this a-b-c right triangle to make an isosceles triangle.

What are all the possible values of N? (Note that any appended triangle may not be degenerate, meaning it must have a positive area. Also, some of the resulting isosceles triangles may be congruent to each other, but they should be counted as distinct if the appended triangles are attached to different sides, or have different positions or orientations.)

Solution

Case I. Scalene

Seem to be the same as $3-4-5$.

$N = 7$.

Case II. $30^{\circ}-60^{\circ}-90^{\circ}$

Except these...they seem to be different.

Since $c = 2a$, Case I.3, Case I.4, and Case II.1 are identical. They happen to be equilateral as well.

$N = 5$.

Case II. $45^{\circ}-45^{\circ}-90^{\circ}$

Case I produces four unique isosceles triangles.

However, since $a = b$, Case II and Case III produce triangles that are the same as the original $45^{\circ}-45^{\circ}-90^{\circ}$ triangle.

$N = 4$.

Answer

$N = 4, 5, 7$.

Rohan Lewis

2024.09.06

Code can be found here.