How High Can You Jump?

Fiddler

The puzzles from the last two weeks have both been about scoring at the Olympics, first in figure skating and then in gymnastics. This week’s puzzle isn’t about scoring, but rather about an event itself.

In the high jump, an athlete’s entire body must clear the bar. However, not every part of their body has to clear the bar at the same time. As a result, athletes arc their bodies over the bar, so that only a fraction of their mass is above the bar at any given time. In fact, athletes can theoretically clear the bar despite their center of mass remaining below the bar throughout the jump.

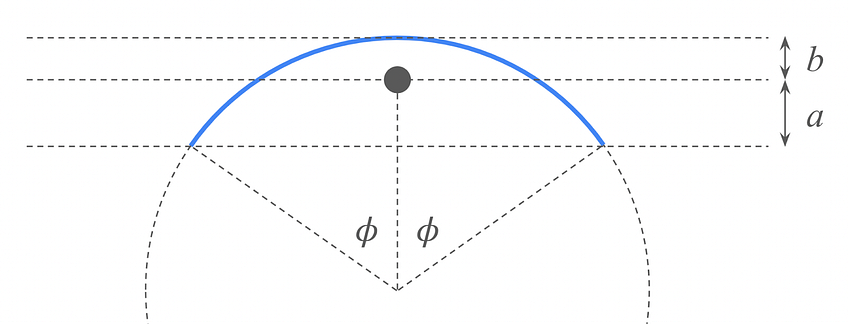
Let’s model the athlete mid-jump as a semicircle, centered over the bar, as shown in the diagram below. For simplicity, assume that their mass is uniformly distributed across the length of their body. The dot in the diagram represents the athlete’s center of mass.

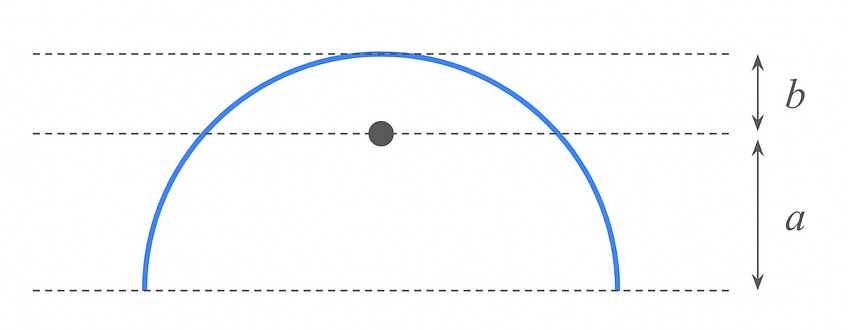
Let a represent the vertical distance between the athlete’s center of mass and their lowest points (presumably their outstretched fingers and toes), and let b represent the vertical distance between the athlete’s center of mass and their highest point (presumably their waist).

What is the ratio a/b?

Solution

Let
$$y = \sqrt{1-x^2} $$
represent the arc of the athlete. The center of mass can be determined by averaging all $y$-values. Thus,
\begin{align*} C &= \frac{1}{1--1} \cdot \int\limits_{-1}^1 \sqrt{1-x^2} dx \\ &= \frac{1}{2} \cdot \left[\frac{\arcsin{x}}{2} + \frac{x \sqrt{1-x^2}}{2}\right]_{-1}^1 \\ &= \frac{1}{2} \cdot \left(\left(\frac{\pi}{4} + 0\right) - \left(-\frac{\pi}{4} + 0\right)\right) \\ &= \frac{\pi}{4} \end{align*}

Answer

\begin{align*} \frac{a}{b} &= \frac{\frac{\pi}{4}}{1-\frac{\pi}{4}} \\ &= \boxed{\frac{\pi}{4-\pi} \approx 3.66} \\ \end{align*}

Extra Credit

Instead of a semicircle, suppose the athlete’s jump is represented by an arc of angle 2𝜙 that is centered over the bar, as shown below:

As before, a represents the vertical distance between the athlete’s center of mass and their lowest points, while b represents the vertical distance between the athlete’s center of mass and their highest point.

As the angle 𝜙 gets very, very small (i.e., in the limit as 𝜙 goes to zero), what value does the ratio a/b approach?

Solution

Similar to above

\begin{align*} C &= \frac{1}{\sin{\phi}--\sin{\phi}} \cdot \int\limits_{-\sin{\phi}}^{\sin{\phi}} \sqrt{1-x^2} dx \\ &= \frac{1}{2\sin{\phi}} \cdot \left[\frac{\arcsin{x}}{2} + \frac{x \sqrt{1-x^2}}{2}\right]_{-\sin{\phi}}^{\sin{\phi}} \\ &= \frac{1}{2\sin{\phi}} \cdot \left(\left(\frac{\phi}{2} + \frac{\sin{\phi} \cdot \sqrt{1-\sin^2{\phi}}}{2} \right) - \left(-\frac{\phi}{2} + \frac{-\sin{\phi} \cdot \sqrt{1-\sin^2{\phi}}}{2} \right)\right) \\ &= \frac{1}{2\sin{\phi}} \cdot \left(\phi + \sin{\phi} \cdot \sqrt{1-\sin^2{\phi}}\right) \\ &= \frac{1}{2\sin{\phi}} \cdot \left(\phi + \sin{\phi}\cos{\phi}\right) \\ &= \boxed{\frac{\phi}{2\sin{\phi}} +\frac{\cos{\phi}}{2}} \\ \end{align*}

Answer

The hands and feet are now at $\cos{\phi}$. Let's find the limit $\frac{a}{b}$...

\begin{align*} &= \lim_{\phi -> 0}\frac{\left(\frac{\phi}{2\sin{\phi}} +\frac{\cos{\phi}}{2}\right) -\cos{\phi}}{1-\left(\frac{\phi}{2\sin{\phi}} +\frac{\cos{\phi}}{2}\right)} \\ &= \lim_{\phi -> 0}\frac{\frac{\phi}{2\sin{\phi}} -\frac{\cos{\phi}}{2}}{1-\frac{\phi}{2\sin{\phi}} - \frac{\cos{\phi}}{2}} \cdot \frac{2\sin{\phi}}{2\sin{\phi}}\\ &= \lim_{\phi -> 0}\frac{\phi - \cos{\phi}\sin{\phi}}{2\sin{\phi} -\phi - \cos{\phi}\sin{\phi}} \\ \end{align*}

Currently, it evaluates to $\frac{0}{0}$. L'Hôpitalling...
\begin{align*} &= \lim_{\phi -> 0}\frac{1 - \left(\cos^2{\phi}-\sin^2{\phi}\right)}{2\cos{\phi} - 1 - (\cos^2{\phi}-\sin^2{\phi})} \\ &= \lim_{\phi -> 0}\frac{1 - \cos{2\phi}}{2\cos{\phi} - 1 - \cos{2\phi}} \\ \end{align*}
It still evaluates to $\frac{0}{0}$. L'Hôpitalling yet again...
\begin{align*} &= \lim_{\phi -> 0}\frac{2\sin{2\phi}}{-2\sin{\phi} + 2\sin{2\phi}} \\ \end{align*}
It still evaluates to $\frac{0}{0}$. L'Hôpitalling yet again...
\begin{align*} &= \lim_{\phi -> 0}\frac{4\cos{2\phi}}{-2\cos{\phi} + 4\cos{2\phi}} \\ &= \frac{4}{-2 + 4} = \boxed{2} \\ \end{align*}

Take a gander!

Rohan Lewis

2024.08.19

Code can be found here.