Can You Hack The Gymnastics?

Fiddler

In artistic gymnastics, competitors earn two subscores: one for difficulty and one for execution. Difficulty, as its name implies, is a measure of how challenging a routine is. While there’s technically no upper bound on the difficulty score, the toughest routines will earn around 6 or 7 points, depending on the apparatus. Meanwhile, execution scores have a maximum value of 10, essentially measuring how cleanly a competitor performed their routine.

What’s weird (to me at least) about gymnastics scoring is that the total score is difficulty plus execution, rather than difficulty times execution.

Why is that weird? Suppose two gymnasts have the same execution score, (say, 8.0 out of 10), but one’s difficulty is 20 percent greater (say, 6.0 to 5.0). You’d expect that gymnast’s overall score to be 20 percent greater, right? But instead, because we’re adding the two subscores, there’s only a 7.7 percent difference in overall score (14.0 to 13.0).

I guess no one is claiming that the total score should scale linearly with both difficulty and execution. But, you know, it really should.

This past week, Brazil’s Rebeca Andrade won the gold medal for her floor routine while American Simone Biles earned the silver. Andrade's total score was 5.9 + 8.266, or 14.166, and Biles’s was 6.9 + 7.233, or 14.133. (Don’t get me started on the rounding.) But if you had multiplied their subscores (like a rational human being), Biles would instead have come out on top, 49.9 to 48.8.

So yeah, the decision to add versus multiply the subscores really matters.

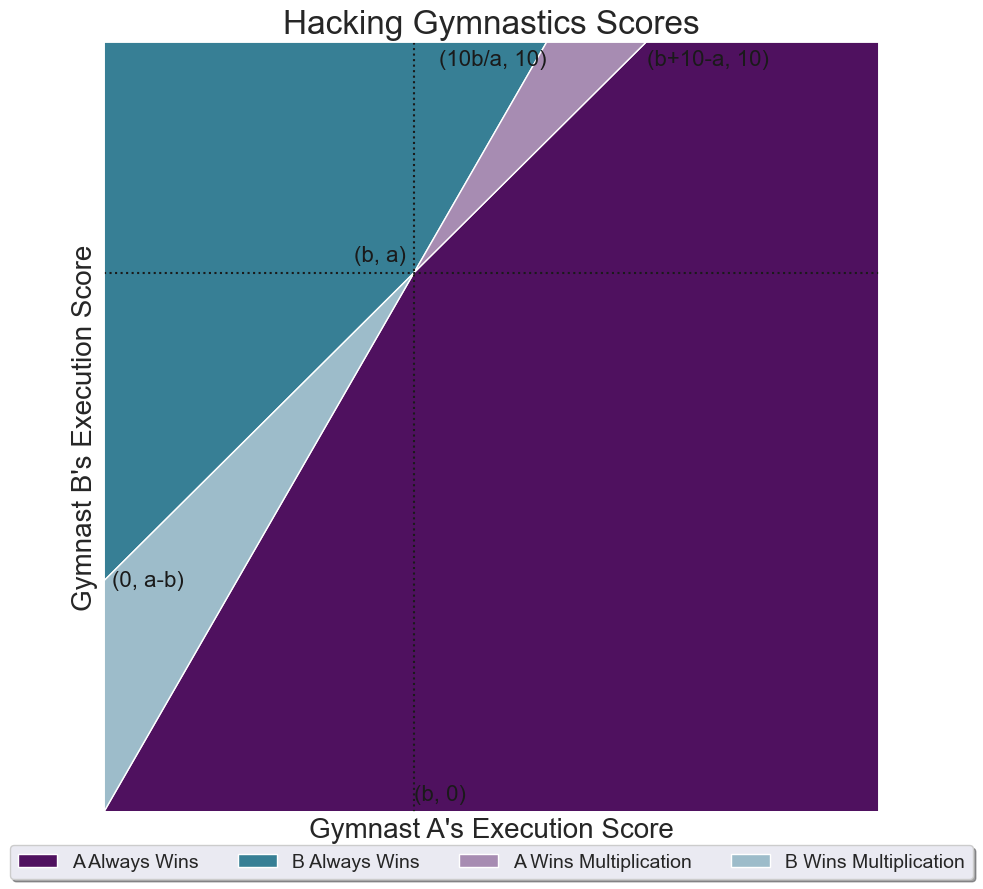
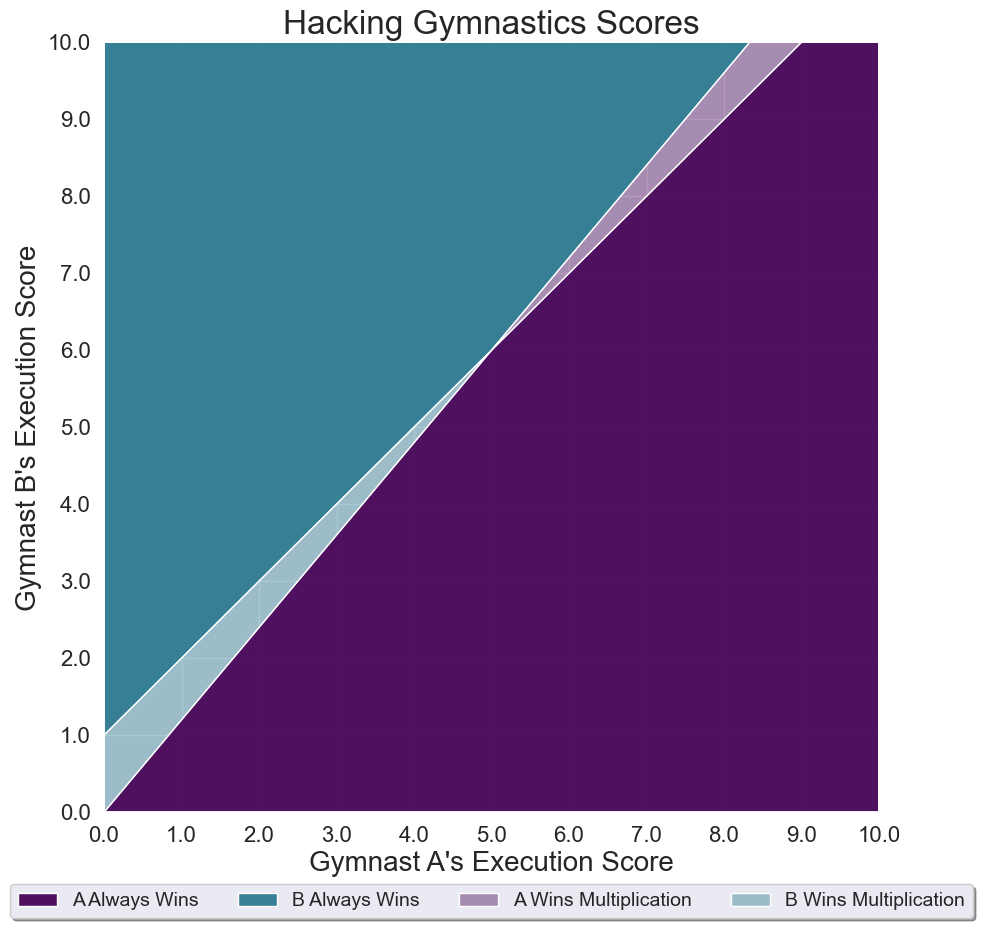
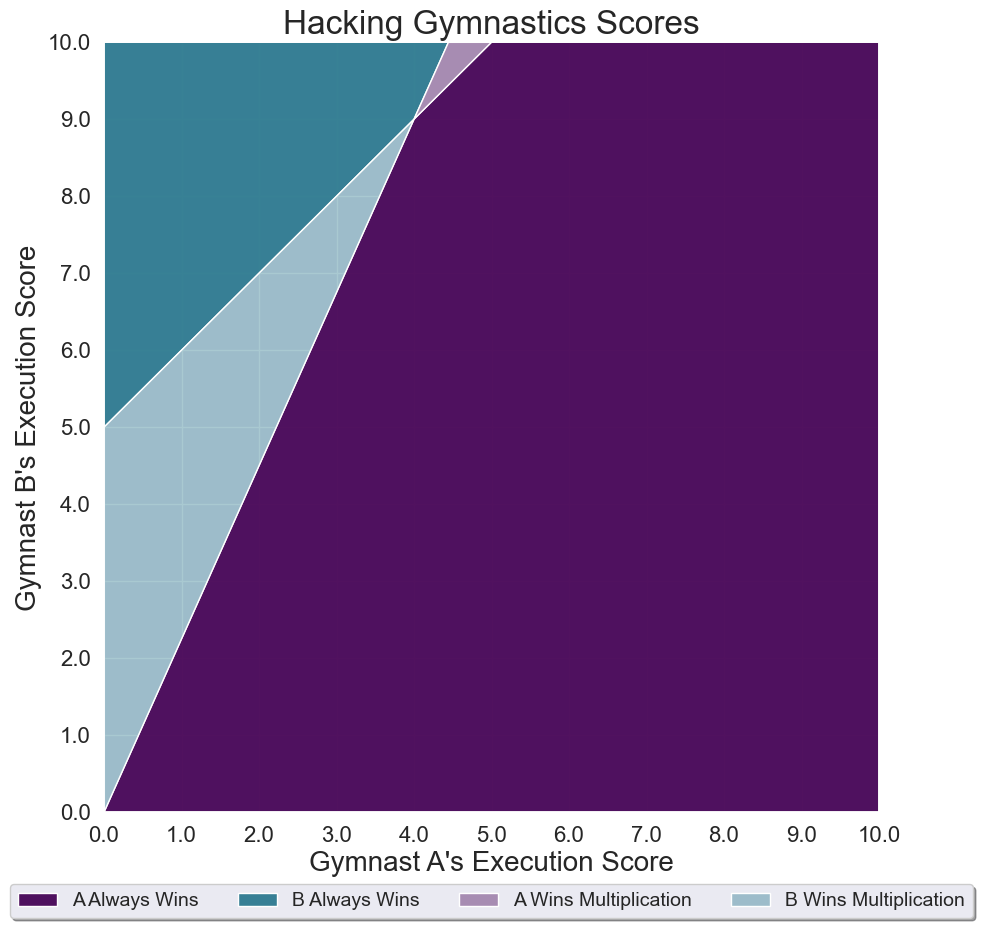
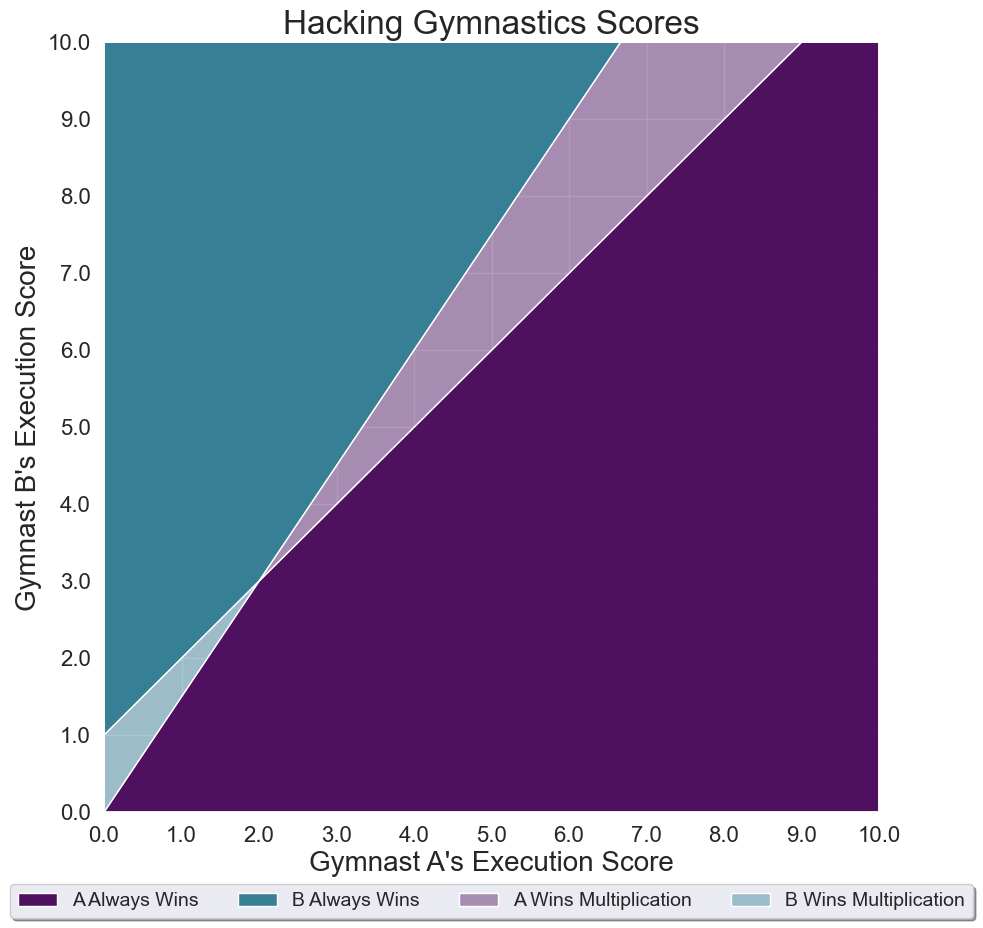
Suppose gymnast A has a difficulty score of 6.0, while gymnast B has a difficulty score of 5.0. If both gymnasts receive independent, random execution scores between 0 and 10 (quite the range, I know), what is the probability that their relative ranking would be the same, regardless of whether the subscores were added or multiplied? (Here, you should assume the execution scores are real numbers that can go to any number of decimal places.)

Solution

Suppose gymnast A has a difficulty score of $a$ and gymnast B has a difficulty score of $b$, where $a \ge b$.

• If gymnast A has an execution score of $b$ and gymnast B has an execution score of $a$ :
  • Both players have the same added score of $a+b$.
  • Both players have the same multiplied score of $a\cdot b$.
  • Denote $(b, a)$ as the center.
• If gymnast A has an execution score of $0$, gymnast B will have a greater multiplied score if their execution score $> 0$.
• If gymnast A has an execution score of $0$, gymnast B will have a greater added score if their execution score $\ge a-b$.
• If gymnast B has an execution score of $10$, gymnast A will have a greater multiplied score if gymnast A's execution score is $\ge \frac{10b}{a}$.
• If gymnast B has an execution score of $10$, gymnast A will have a greater added score if gymnast A's execution score is $\ge b+10-a$.

This can be summarized in the diagram below...that will be used for the Extra Credit.

The area of the light teal region is,

$$\frac{1}{2}(a-b)\cdot b = \boxed{\frac{ab-b^2}{2}}$$

The area of the light purple region is,

$$\frac{1}{2}\left((b+10-a) - \frac{10b}{a}\right)(10-a) = \boxed{\frac{a^2}{2} - \frac{ab}{2} + 10b - 10a - \frac{50b}{a} + 50}$$

For the given problem, we have,

Substituting $a = 6$ and $b = 5$,

$$\frac{6\cdot 5-5\cdot b^2}{2} = \frac{5}{2}$$$$\frac{6^2}{2} - \frac{6\cdot 5}{2} + 10(5) - 10(6) - \frac{50(5)}{6} + 50 = \frac{4}{3}$$

Answer

The darker two regions denote consistent scoring regardless of arithmetic operation,

\begin{align*} &= \frac{100 - \frac{5}{2} - \frac{4}{3}}{100} \\ &= \frac{577}{600} \approx \boxed{96.167 \%} \\ \end{align*}

Extra Credit.

In addition to their execution scores, now assume that both difficulty scores are now also independent, random values between 0 and 10 (again, quite the range).

What is the probability that their relative ranking would be the same, regardless of whether the subscores were added or multiplied? (Again, assume all subscores are real numbers that can go to any number of decimal places.)

Solution

Suppose gymnast A has a difficulty score of $a$ and gymnast B has a difficulty score of $b$, where $a \ge b$, as mentioned above. The probability that their relative ranking is the same can be found by,

• Taking the sum of both triangular regions.
• Integrating with respect to $b$ from $0$ to $a$.
• Integrating with respect to $a$ from $0$ to $10$.
• Multiplying by 2 to account for $b>a$, and divide by $100$ to get average.
• Subtracting from 100 to get the area of regions where the relative ranking is the same.

\begin{align*} A &= 100 - \frac{2}{100}\int\limits_0^{10} \int\limits_0^a \left(\frac{ab-b^2}{2} + \frac{a^2}{2} - \frac{ab}{2} + 10b - 10a - \frac{50b}{a} + 50 \right) db\text{ }da \\ &= 100 - \frac{1}{50}\int\limits_0^{10} \int\limits_0^a \left(\frac{a^2}{2} - \frac{b^2}{2} + 10b - 10a - \frac{50b}{a} + 50 \right) db\text{ }da \\ &= 100 - \frac{1}{50}\int\limits_0^{10} \left[\frac{a^2b}{2} - \frac{b^3}{6} + 5b^2 - 10ab - \frac{25b^2}{a} + 50b \right]_0^a da \\ &= 100 - \frac{1}{50}\int\limits_0^{10} \left(\frac{a^3}{2} - \frac{a^3}{6} + 5a^2 - 10a^2 - 25a + 50a \right) da \\ &= 100 - \frac{1}{50}\int\limits_0^{10} \left(\frac{a^3}{3} - 5a^2 + 25a \right) da \\ &= 100 - \frac{1}{50}\left[\frac{a^4}{12} - \frac{5a^3}{3} + \frac{25a^2}{2} \right]_0^{10} da \\ &= 100 - \frac{1}{50} \cdot \frac{1250}{3} = \frac{275}{3} \\ \end{align*}

Answer

$$\frac{275}{3} \approx \boxed{91.67\%}$$

Here are some additional images...

Rohan Lewis

2024.08.12