Can You Spy on the Infinite Corridor?

Fiddler

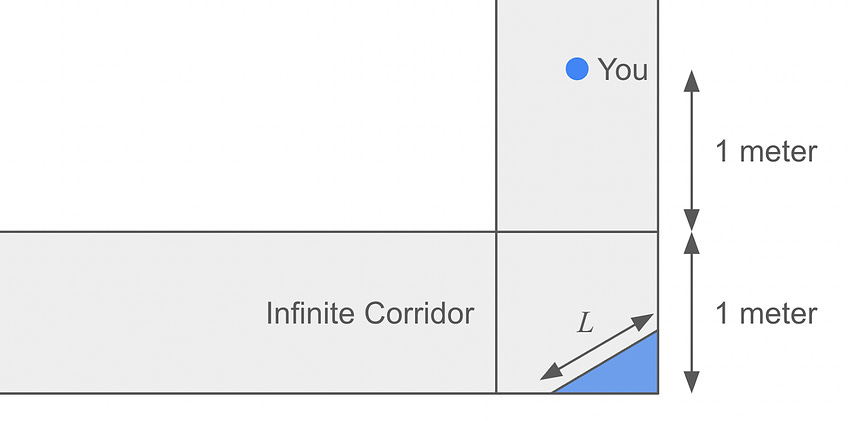
You’re a senior member of the Fiddler Spy Agency, and you’ve infiltrated the enemy base, as diagrammed below. You currently find yourself standing in the middle of a narrow corridor, 1 meter wide. You are 1 meter away from a square turn in the corridor, around which is a very long “infinite corridor” (so named because, well, it’s very long.)

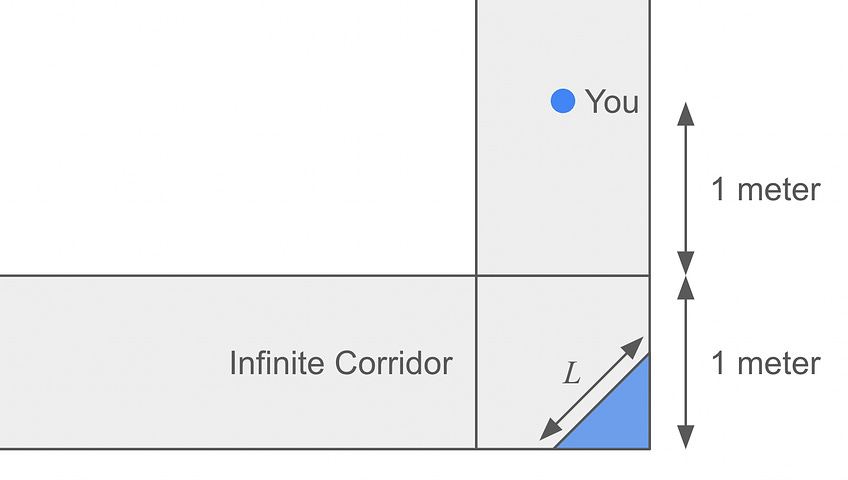
Importantly, there’s a flat mirror placed at a 45 degree angle in the far corner of the turn, as shown above. The mirror forms a 45-45-90 right triangle with that corner, such that its hypotenuse (i.e., the length of the mirror) is L.

For different values of L, you can “spy on” different sections of the infinite corridor. A given point in the infinite corridor can be spied upon if there is some location on the mirror that reflects light from that point to where you are standing.

What is the minimum value of L such that the mirror allows you to spy on the entire infinite corridor? (Note that this is a puzzle in two, rather than three, dimensions.)

Solution

1. Set the given diagram on a coordinate plane where the square corner between the corridors has coordinates $(0,0)$, $(0,1)$, $(1,1)$, and $(1,0)$.
2. Define the mirror's surface as the equation $x-y = a$. This gives the points $(a, 0)$ and $(1, 1-a)$.
3. The smallest mirror will have $(1, 1-a)$ as the reflection point between you and the upper left corner, $(0, 1)$.
4. Draw a perpendicular from each of $(0,1)$ and $(\frac{1}{2}, 2)$ to the line $x-y = a$.
5. The respective points of intersection are $(\frac{1+a}{2}, \frac{1-a}{2})$ and $(\frac{5}{4} + \frac{a}{2}, \frac{5}{4} - \frac{a}{2})$.

As long as $a \le \dfrac{1}{2}$, the bottom wall will be visible.

Since the two triangles are similar, the ratio of the legs forms a proportion:

\begin{align*} \dfrac{\dfrac{1+a}{2}\sqrt{2}}{\dfrac{1-a}{2}\sqrt{2}} &= \dfrac{\dfrac{3+2a}{4}\sqrt{2}}{\dfrac{1+2a}{4}\sqrt{2}} \\ \dfrac{1+a}{1-a} &= \dfrac{3+2a}{1+2a} \\ 2a^2+3a+1 &= -2a^2-a+3 \\ 2a^2+2a-1 &= 0 \\ a &= \dfrac{-2\pm\sqrt{4+8}}{4} = \boxed{\dfrac{\sqrt{3} - 1}{2}} \\ \end{align*}

Answer

The base of the mirror is:
$$1-a = \dfrac{3-\sqrt{3}}{2}$$
Multiplying by $\sqrt{2}$:
$$L = \boxed{\dfrac{3-\sqrt{3}}{\sqrt{2}}} \approx \boxed{0.8966}$$
Take a gander!

Extra Credit.

Now suppose the flat mirror is no longer constrained to be at a 45 degree angle with the corner. That said, it must still be flush against the corner so that it forms a right triangle, as illustrated below:

Once again, what is the minimum length of the hypotenuse L such that the mirror allows you to spy on the entire infinite corridor?

Rohan Lewis

2024.07.08

Code can be found here.