How Many Ways Can You Tile the Tilted Square?¶

Fiddler¶

From high schooler Taran Knutson comes a puzzle that was originally inspired by the Catalan numbers:

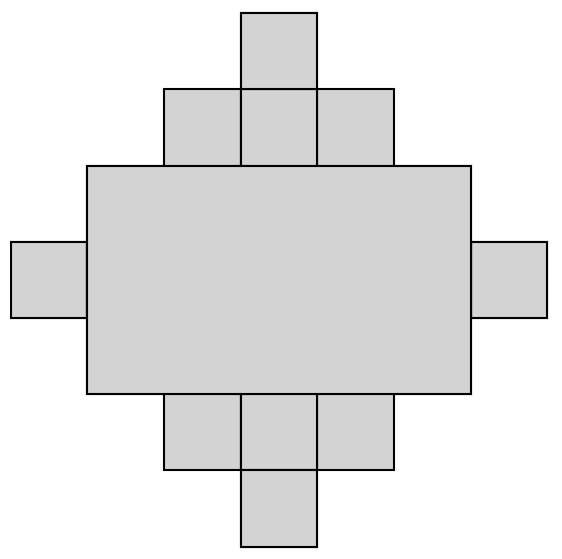
Consider the following array of 25 squares: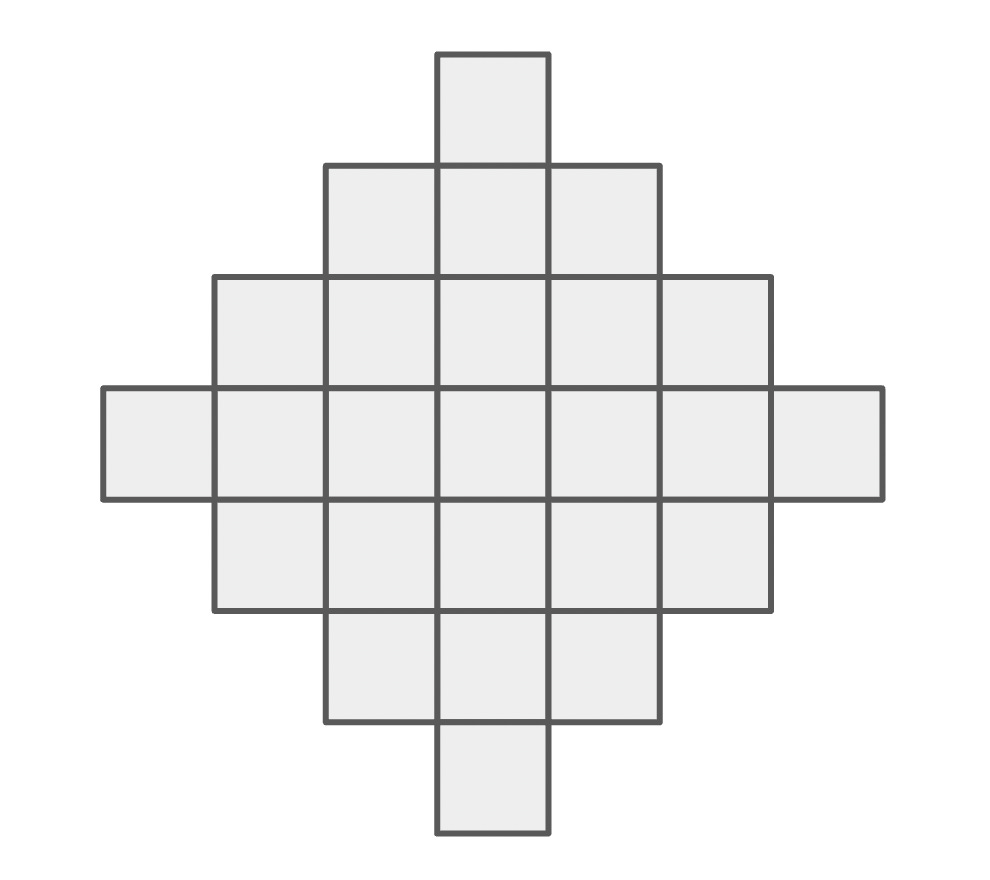

You are filling the array with rectangles by repeating the following two steps:

  1. Select one of the 12 squares along the outer perimeter that has not yet been selected as part of a rectangle.

  2. Form the largest rectangle you can that includes the square you just selected and other squares that are not yet part of any such rectangle.

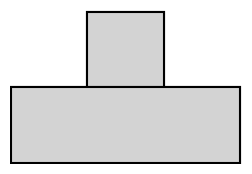
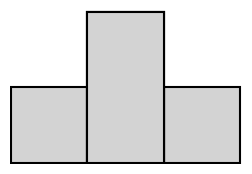
You repeat these steps until every square along the perimeter has been selected. Here are two final states you might encounter:

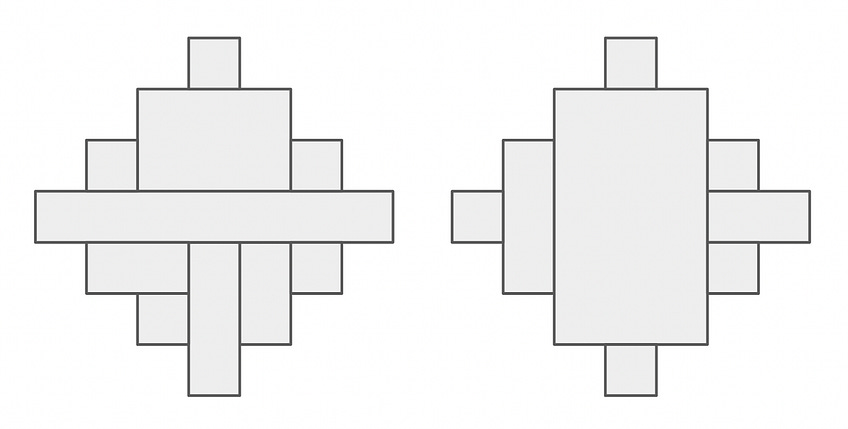
How many distinct final states are possible? (Note: States that are rotations or reflections of each other should be counted as distinct.)

Solution¶

The original array can initially be tiled two ways. Each way has a horizontal and vertical orientation.

First Tile First Option¶

The top and bottom can be split one of three ways.


The top tile can be tiled again.

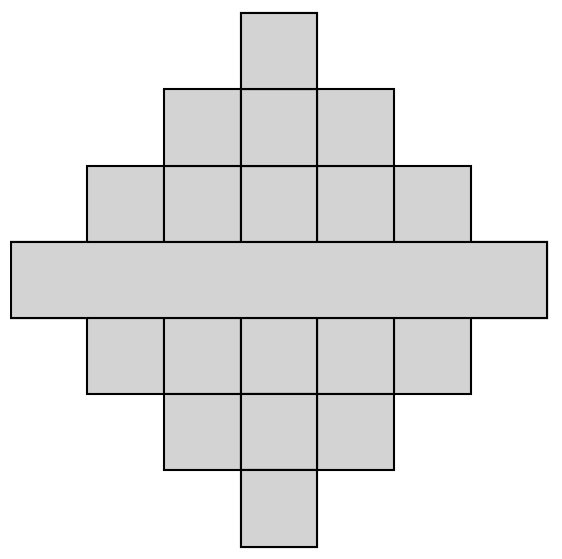
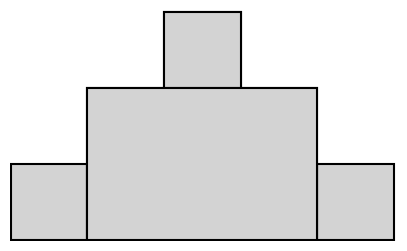
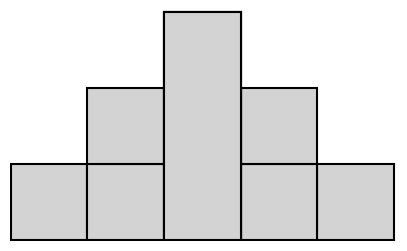The left and right tiles can be tiled again.

First Tile Second Option¶

The top and bottom can be split one of two ways.

Answer¶

There are $\boxed{106}$ tilings.

Extra Credit¶

The arrays in this week’s Fiddler had four squares along each outer “edge.” For Extra Credit, consider a slightly larger array, with five squares along each edge:

As before, you are filling the array with rectangles by repeatedly selecting one of the outermost squares and forming a rectangle that includes as many “un-rectangled” squares as possible.

How many distinct final states are possible? (Can you find a general formula for an array with N squares along each outer edge?)

Solution¶

Similar to above, I did successive tilings. There were three first tile placements. Then, using the 'half arrays' and 'quarter arrays', more counting was done.

I ran code that counted all the methods. There is a different pattern for even and odd numbers.

Answer¶

There are $\boxed{2,987}$ tilings.

Rohan Lewis¶

2024.06.17¶

Code can be found here.