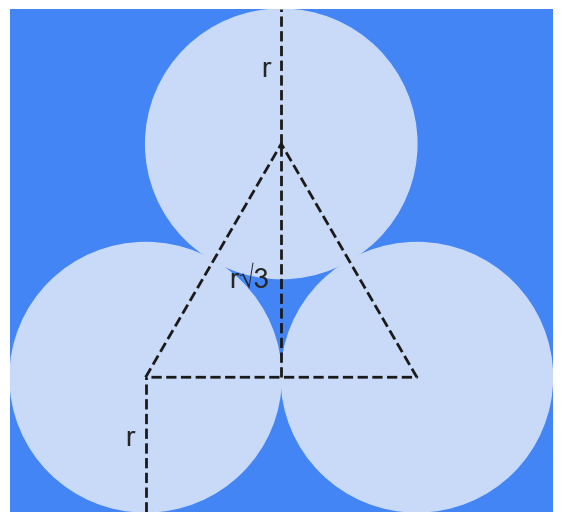
Can You Pack the Circles?

Fiddler

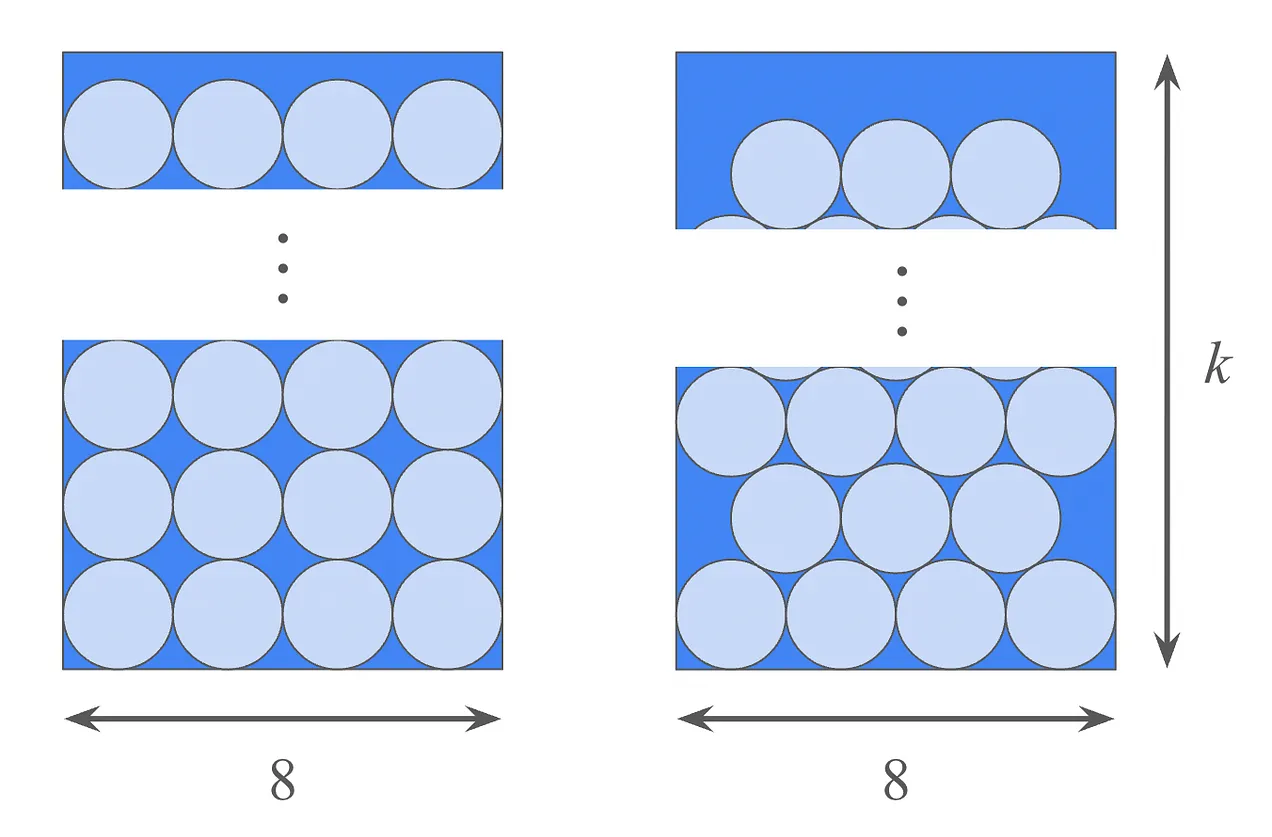
You want to pack four rows of unit circles into a rectangle with a base of 8. You’re considering two strategies for packing:

1. Square packing. In this case, four rows of circles each are packed in an array of squares.

2. Hexagonal packing. In this case, the bottom row has four circles, and higher rows alternate between having three and four circles.

The following diagram shows the square-packed and hexagonal-packed rectangles on the left and right, respectively:

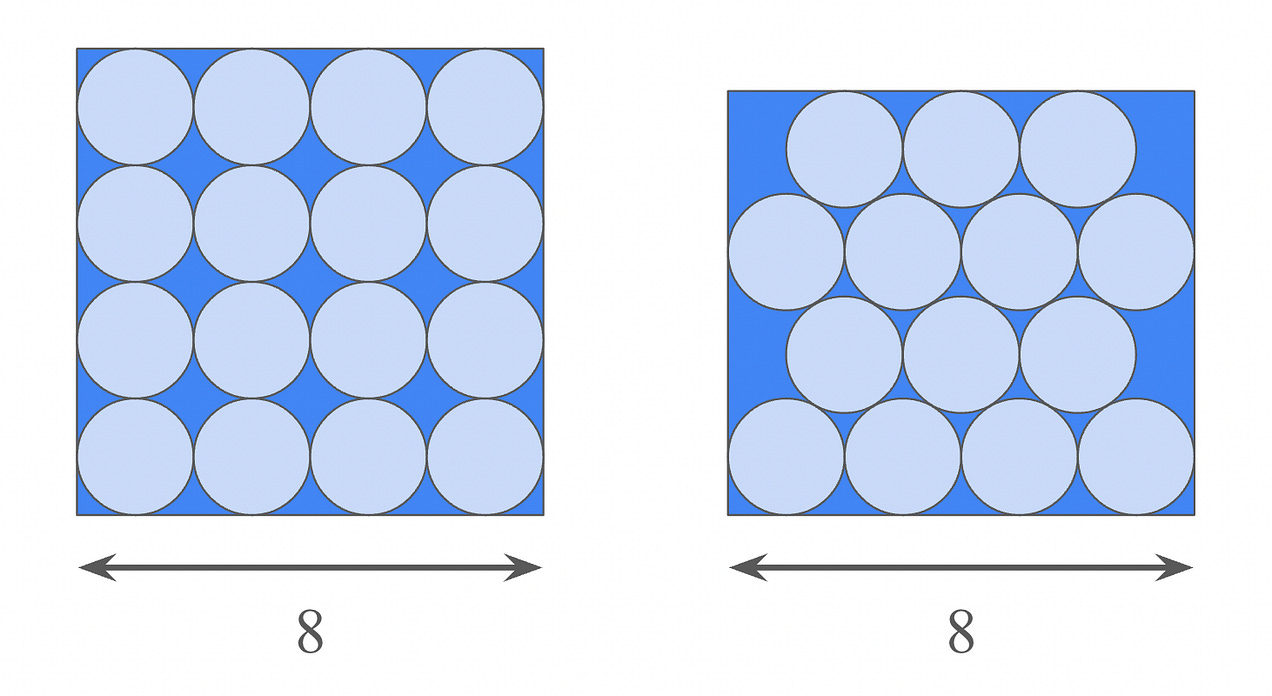
While the bases of both rectangles are 8, their heights are as small as possible such that the circles all fit.

Which packing strategy—square or hexagonal—is more efficient for packing these four rows? In other words, which packing results in a greater number of circles packed per unit of rectangular area?

Solution

The square packed method will always result in a ratio of $\boxed{\dfrac{1}{4} \text{ circle per unit area}}$, provided the dimensions are multiples of 2.

The area of the hexagonal packed rectangle can be found from the following diagram :

We can see that the height of the rectangle is $2 + (c_k-1)\sqrt{3}$, where $c_k$ is the height, in circles.

The area of the rectangle above is $\dfrac{14}{8 \cdot \left(2 + 3\sqrt{3}\right)} \approx \boxed{0.2431}$.

Answer

Square packed is more efficient.

Extra Credit

Over large spaces, hexagonal packing of unit circles is more efficient than square packing. But instead of a large space, suppose you have an 8×k rectangle.

Assume that both packing strategies start with four circles on the bottom row of the rectangle. Square packing adds additional rows of four circles, one on top of the other, until there is insufficient room at the top of the rectangle. Meanwhile, hexagonal packing adds additional rows that alternate between three and four circles, one on top of the other, until there is insufficient room at the top of the rectangle. Here are diagrams of both packing strategies in an 8×k rectangle (note that the hexagonal-packed rectangle can have either three or four circles in the top row):

At some point, hexagonal packing will always be more efficient than square packing. What is the minimum value of k such that, for all heights greater than or equal to k, hexagonal packing is strictly more efficient than square packing?

Solution

Lets look at all $j x k$ rectangles. As mentioned in the Fiddler above, the square packed method will always result in a ratio of $\dfrac{1}{4}$ circle per unit area. The focus will be on hexagonal packing.

Let $c_j$ and $c_j$ be the number of circles across the width and height, respectively.

$j = 2 \cdot c_j$ and $k = 2 + (c_k-1)\sqrt{3}$ from above.

Define rows that have $c_j$ circles as full. There are $\bigg\lceil\dfrac{c_k}{2}\bigg\rceil$ of these rows.

Define rows that have $c_j-1$ circles as partial. There are $\bigg\lfloor\dfrac{c_k}{2}\bigg\rfloor$ of these rows.

The number or circles per unit area is thus:
$$\boxed{\dfrac{c_j\cdot \bigg\lceil\dfrac{c_k}{2}\bigg\rceil + (c_j-1)\cdot\bigg\lfloor\dfrac{c_k}{2}\bigg\rfloor}{2c_j \cdot \left(2 + (c_k-1)\sqrt{3}\right)}}$$
However, this is if the circle packing is to the top of the rectangle. If k is slightly less than this value, then the top row of circles would not exist. Thus, substitute and solve

$$\dfrac{1}{4} \le \dfrac{4\cdot \bigg\lceil\dfrac{c_k-1}{2}\bigg\rceil + 3\cdot\bigg\lfloor\dfrac{c_k-1}{2}\bigg\rfloor}{8 \cdot \left(2 + (c_k-1)\sqrt{3}\right)}$$

Using code, I found that for $c_j = 4$, $c_k = 111$ yields a right side of $\approx 0.249967$. Every value of $c_k > 111$ will yield a right side $> 0.25$.

Answer

Substituting in for $k$,

$$k = \boxed{2+110\sqrt{3}} \approx \boxed{192.53}$$

I tried to make a heatmap to visualize this but the numbers didn't fit an aesthetic view...

As the height and width get very large, the packing approaches $\dfrac{1}{2\sqrt{3}} \approx 0.2887$, as shown by the image below.

Rohan Lewis

2024.06.17

Code can be found here.