Answer¶
$$\dfrac{2880+21600+50400}{3628800} = \boxed{\dfrac{13}{630} \approx 2.06\%}$$
Playing safe requires one to pass...a lot!
You’re playing a modified version of blackjack, where the deck consists of exactly 10 cards numbered 1 through 10. Unlike traditional blackjack, in which the ace can count as 1 or 11, the 1 here always has a value of 1.
You shuffle the deck so the order of the cards is completely random, after which you draw one card at a time. You keep drawing until the sum of your drawn cards is at least 21. If the sum is exactly 21, you win! But if the sum is greater than 21, you “bust,” or lose.
What are your chances of winning, that is, of drawing a sum that is exactly 21?
There are $10! = 3,628,800$ unique deck orders. I ran code to determine which ones have a sum of $21$ from consecutive cards at the top of the deck.
$635,040$ decks achieve a sum of exactly $21$.
$$\dfrac{635040}{3628800} = \boxed{\dfrac{7}{40} = 17.5\%}$$Playing for 21 or bust is a risky strategy. From this moment on, you decide to be risk averse.
You’re playing the same modified version of blackjack again, but this time, whenever there’s even the slightest chance you could bust on the next card, you quit the round and start over. On average, how many rounds should you expect to start until you finally win?
To continue, there must be $0$ chance of you getting over $21$. That means the maximum value of the card remaining in the deck must be less than the difference of $21$ and the sum of the cards currently in hand. There are three cases.
$1,2,3,5,10$ would allow the first four cards to sum to 11 and be safe for not busting on the fifth.
In order for $9$ to be the fifth card, $10$ and three cards must sum to $12$, which is impossible. Thus, there are no other possibilities.
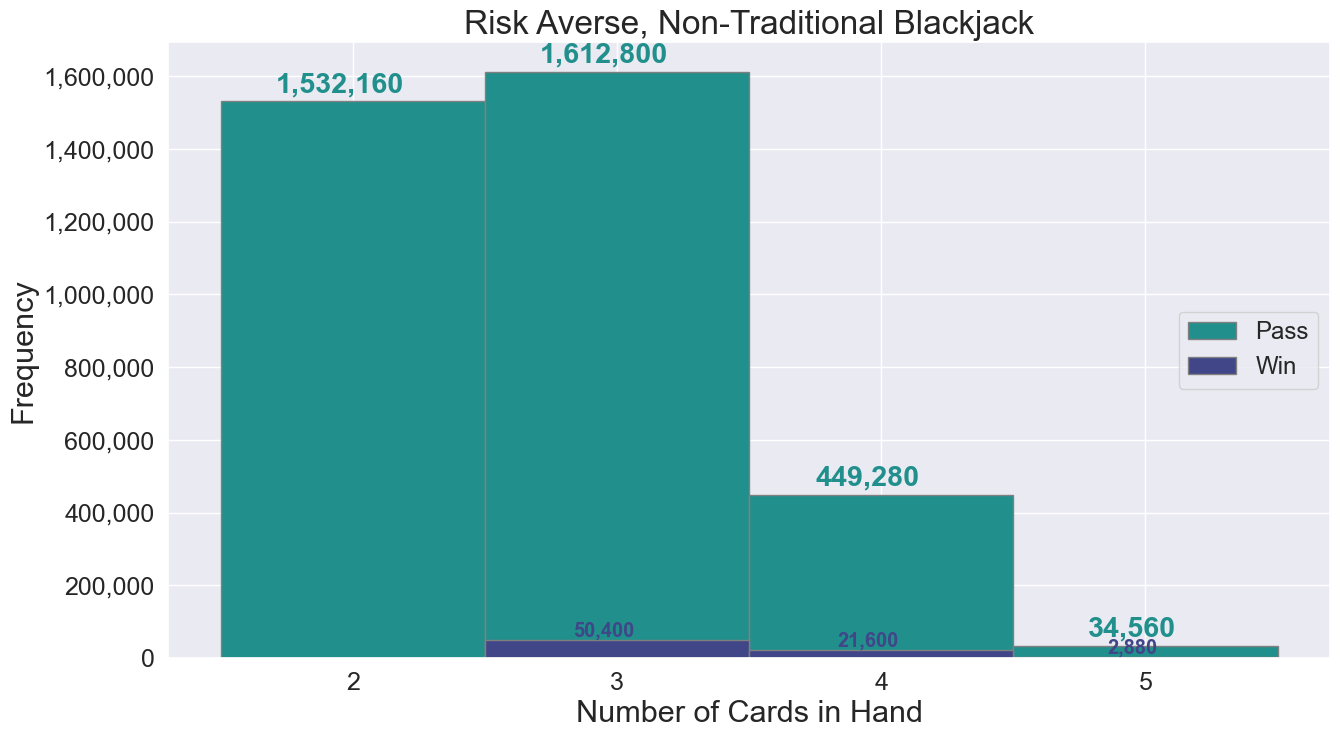
There are $4! \cdot 1 \cdot 5! = \boxed{2,880}$ hands.
The following five possibilities,
would allow the first three cards to sum to 11 and be safe for not busting on the fourth.
In order for $9$ to be the fourth card, $10$ and two cards must sum to $12$, which is impossible. Thus, there are no other possibilities.
There are $5 \cdot 3! \cdot 1 \cdot 6! = \boxed{21,600}$ hands.
The following four possibilities,
would allow the first two cards to sum to 11 and be safe for not busting on the fourth.
In order for $9$ to be the third, $10$ and one card must sum to $12$, which is $2,10,9$.
$8$ cannot be the third, as $9 + 10 = 19$.
There are $5 \cdot 2! \cdot 1 \cdot 7! = \boxed{50,400}$ hands.
Playing safe requires one to pass...a lot!
