Answer¶
Suppose you have infinitely many 3-by-3 cm tiles and infinitely many 5-by-5 cm tiles. You want to use some of these tiles to precisely cover a square whose side length is a whole number of centimeters. Tiles may not overlap, and they must completely cover the larger square, without jutting beyond its borders.
What is the smallest side length this larger square can have, such that it can be precisely covered using at least one 3-by-3 tile and at least one 5-by-5 tile?
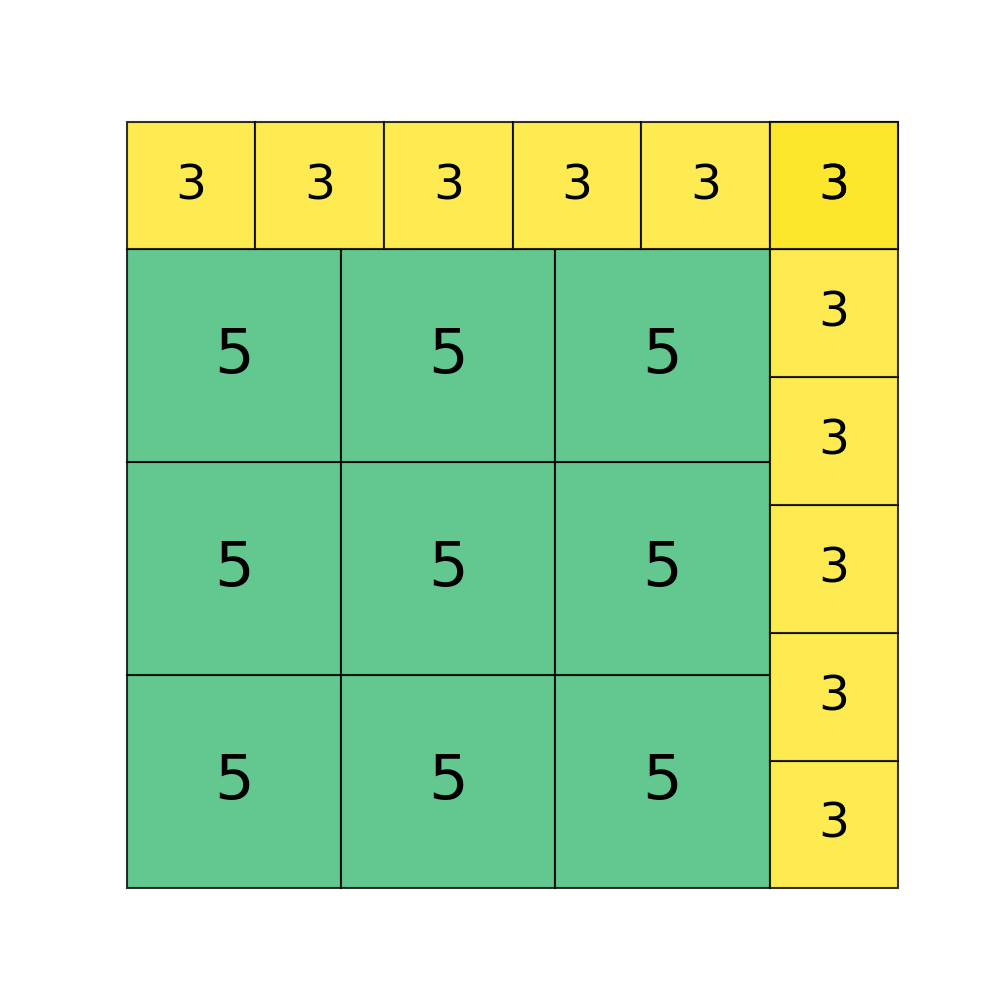
In order for there to be no overlap or jutting beyond borders, I considered $lcm(3,5) = 15$.
Creating a 15-by-15 tiles with nine 5-by-5 tiles, and adding a 3cm border with eleven 3-by-3 tiles yields a side length of 18.

This week’s Extra Credit is a personal favorite of high schooler Linus Tang. Linus was a Finalist of the 2024 Regeneron Science Talent Search, where he presented his research on measures of peripherality (the opposite of centrality) in graphs. He was also a Gold Award winner at the 2024 USA Math Olympiad. Outside of his impressive academic accomplishments, Linus is also an avid player of Go.
Here’s is Linus’s puzzle:
This time, you have an infinite supply of square tiles for each odd whole number side length (as measured in centimeters) greater than 1 cm. In other words, you have infinitely many 3-by-3 cm tiles, infinitely many 5-by-5 cm tiles, infinitely many 7-by-7 cm tiles, and so on.
You want to use one or more of these tiles to precisely cover a square whose side length is N cm, where N is an integer. Once again, tiles may not overlap, and they must completely cover the larger square without jutting beyond its borders. (Before you ask—yes, all odd values of N result in squares that can be covered with a single tile.)
What is the largest integer N for which this task is not possible?
All odd values of $N$ result in squares that can be covered by a single tile. Furthermore, any value of $N = nk$, or a multiple of an odd number, can be precisely covered by $k^2$ squares of side length $n$.
The only values of $N$ unaccounted for are powers of 2.
I again considered $lcm$, but this time I am looking for rectangles.
An 8-by-15 rectangle can be created from a row of five 3-by-3 and three 5-by-5.
Extending this, there are an infinite number of rectangles in the form $(3a + 5b)$-by-$15$ created from $a$ rows of five 3-by-3 and $b$ rows of three 5-by-5.
Extending this again, there are an infinite number of rectangles in the form $(ax + by)$-by-$xy$ created from $a$ rows of $y$ x-by-x and $b$ rows of $x$ y-by-y, where $gcd(x,y) \ne 1$.
Solving for one side of the square, $xy + ax + by + xy = 2^m$ for some integer $m$. Using code, the two solutions with the smallest values are for $m = 6$
However, the 34-by-15 can be halved. This yields a 32-by-32 square that can be completely covered by odd tiles.
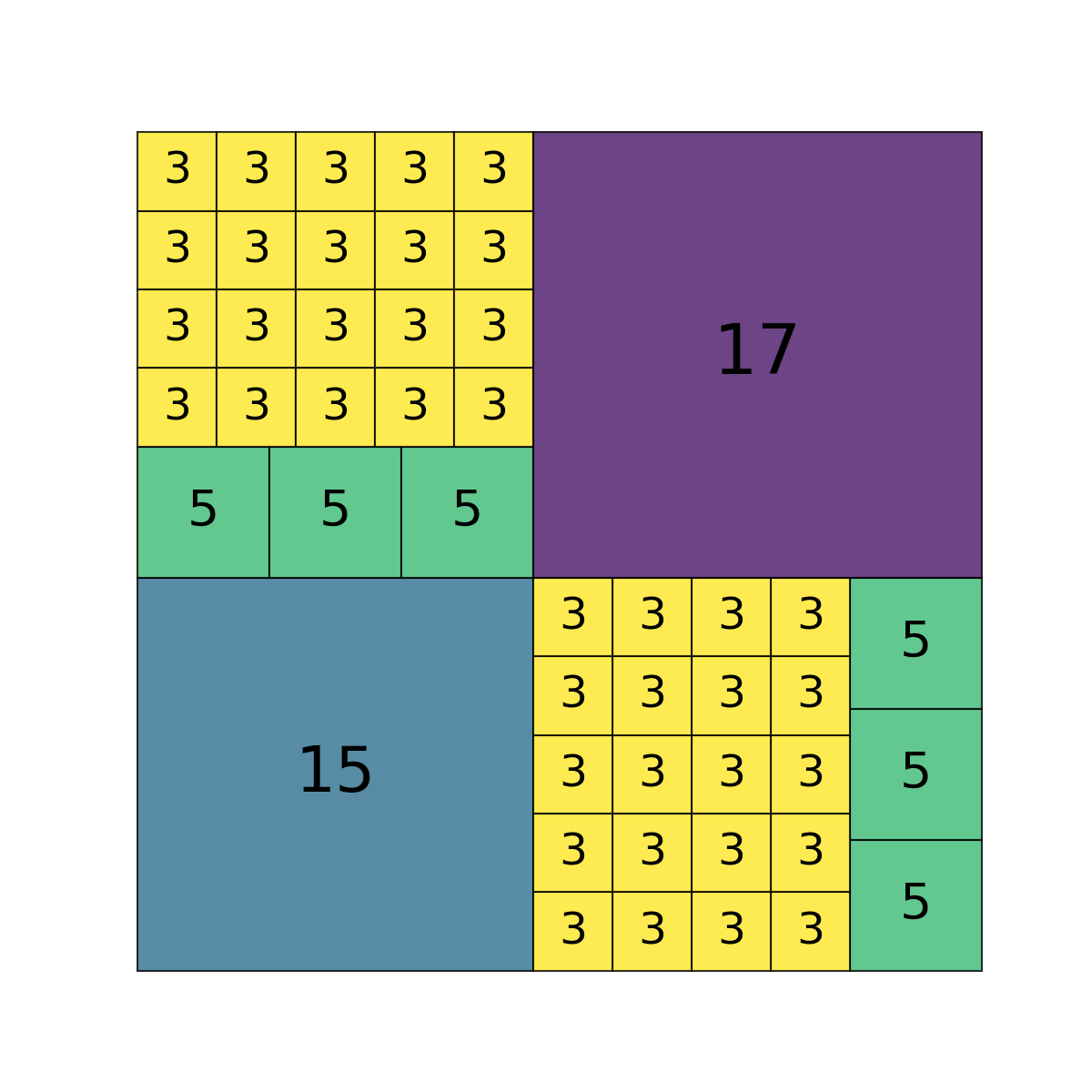
Every $2^m$ square, $m \ge 5$, can now be tiled, using $4^{m-5}$ of the 32-by-32 decomposition above.
$m = 4$ yields 16, which is too small as it is only 1 greater than $lcm(3,5) = 15$.
Therefore $16$ is the largest square that cannot be covered by odd tiles.