This week’s puzzle is based on a suggestion from Stephen Cranston. Some of you may no doubt be familiar with this one, but it was new to me (I think?), and it was so juicy that I just had to share it.
You and a friend each have a standard deck with 52 cards. You thoroughly shuffle your deck, while your friend thoroughly shuffles theirs. Then, you both draw cards one at a time. If the first card you draw is the same as the first card your friend draws, you lose! Otherwise, you draw again. If the next card you draw is the same as the next card your friend draws, you lose! Otherwise … and so on.
If the two of you can make it through your entire decks without ever drawing the same card at the same time, you both win. Otherwise, you both lose.
What is the probability that you and your friend will win this collaborative game?
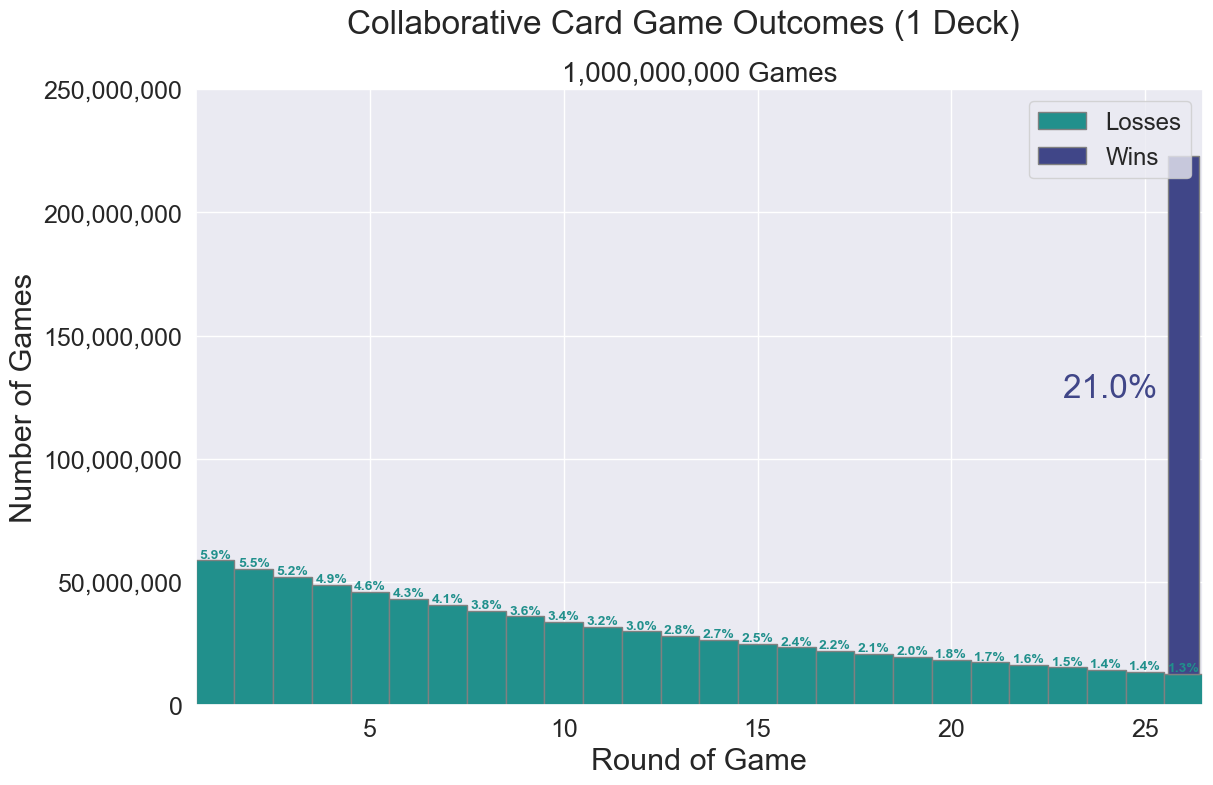
The probability one card matches the other is $\dfrac{52}{52} \cdot \dfrac{3}{51} \approx 0.0588235$.
$\dfrac{48}{51}$ of the time the first two cards are different. $44$ out of the remaining $50$ cards would not match with the first two and $6$ would. The probability the second draw round cards match each other is $\dfrac{48}{51} \big(\dfrac{44}{50} \cdot \dfrac{3}{49} + \dfrac{6}{50} \cdot \dfrac{2}{49}\big) \approx 0.0553181$.
I could not think of a formula to determine this down to the $26^{\text{th}}$ pair of cards, so I created code that started with a deck of cards and did the following :

Out of $1,000,000,000$ games, $210,203,317$ were wins, or $\approx 21.0\%$.
If you’ve already seen some version of this week’s Fiddler before, then you should try your hand at this variant:
Once again, you and your friend both have standard decks of 52 cards. This time, you first combine them into a single deck with 104 cards, and you thoroughly shuffle it. Then, you randomly split this back into two decks with 52 cards each—one for you, and one for your friend.
At this point, you continue as before, with each of you drawing one card at a time. If the two of you can make it through your entire decks without ever drawing the same card at the same time, you both win. Otherwise, you both lose.
What is the probability that you and your friend will win this collaborative game?
The probability one card matches the other is $\dfrac{104}{104} \cdot \dfrac{7}{103} \approx 0.0679611$.
$\dfrac{96}{103}$ of the time the first two cards are different. $88$ out of the remaining $102$ cards would not match with the first two and $14$ would. The probability the second draw round cards match each other is $\dfrac{96}{103} \big(\dfrac{88}{102} \cdot \dfrac{7}{101} + \dfrac{14}{102} \cdot \dfrac{6}{101}\big) \approx 0.0633301$.
Utilizing my code with a different deck size, I achieved:
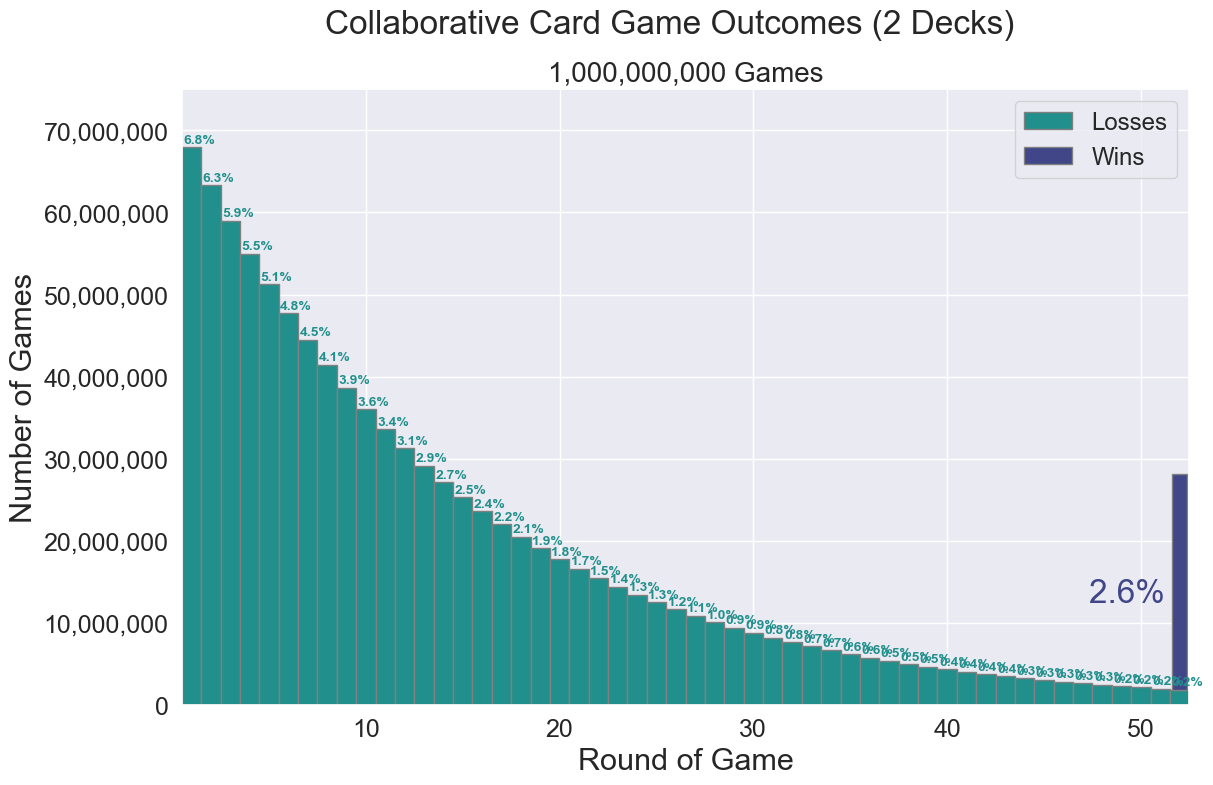
Out of $1,000,000,000$ games, $26,243,360$ were wins, or $\approx 2.62\%$.