Like many folks around the United States and Mexico, I had the chance to see a mostly-occluded sun this past Monday. (It’s pretty remarkable that the sun and the moon have such similar apparent sizes in the sky.)
But instead of one circular shape obscuring another, what if there were two such shapes? In other words, suppose you have two congruent circles that, together, completely cover another circle. How small could those two congruent circles be?
The answer to this version of the “disk covering problem” turns out to be rather boring: Both circles must be the same size as the one they cover. In the past, when circles have proven uninteresting for one reason or another, I turn to ellipses. (How cool would it be to have a moon shaped like Haumea?)
So suppose you have two congruent ellipses that, together, cover a unit circle (i.e., a circle with radius 1). These ellipses can have any eccentricity you like, but they must be congruent to each other.
What is the smallest possible area one of these ellipses can have, such that they completely cover the circle?
The sum of the distances from the foci to a point is the major axis. Thus,
$$2b = \sqrt{\big(\left(1-a\right)-0\big)^2 +\left(-\sqrt{b^2-a^2}-1\right)^2} + \sqrt{\big(\left(1-a\right)-0\big)^2 +\left(\sqrt{b^2-a^2}-1\right)^2 }$$
$$2b = \sqrt{\left(a^2-2a+1\right) + \left(b^2-a^2 + 2\sqrt{b^2-a^2} + 1\right)} + \sqrt{\left(a^2-2a+1\right) + \left(b^2-a^2 - 2\sqrt{b^2-a^2} + 1\right)}$$
$$2b = \sqrt{b^2 - 2a + 2 + 2\sqrt{b^2-a^2}} + \sqrt{b^2 - 2a + 2 - 2\sqrt{b^2-a^2}}$$
Squaring both sides,
$$2b^2 + 4a - 4 = 2\sqrt{\left(b^2 - 2a + 2 + 2\sqrt{b^2-a^2}\right) \cdot \left(b^2 - 2a + 2 - 2\sqrt{b^2-a^2}\right)}$$
Dividing by 2 and squaring both sides,
$$ b^4 + 4ab^2 + 4a^2 - 4b^2 - 8a + 4= b^4 -4ab^2 + 4a^2 + 4b^2 - 8a + 4 - 4b^2 +4a^2$$
$$8ab^2 - 4b^2 = 4a^2$$
$$b = \dfrac{a}{\sqrt{2a-1}}$$
Since the area of an ellipse is $\pi ab$, substitute to get
$$A = \dfrac{\pi a^2}{\sqrt{2a-1}}$$
Taking the derivative,
$$0 = \dfrac{\big((2a-1)^{\frac{1}{2}} \cdot 2a\big) - \big(a^2 \cdot (2a-1)^{-\frac{1}{2}} \cdot \frac{1}{2} \cdot 2\big)}{2a-1}$$
Multiplying by $\dfrac{(1-2a)^{\frac{1}{2}} }{(1-2a)^{\frac{1}{2}} }$,
$$= \dfrac{\big((2a-1) \cdot 2a\big) - \big(a^2\big)}{(2a-1)^{\frac{3}{2}}}$$
$$ = 4a^2-2a-a^2 = 3a^2-2a$$
(You probably know what’s coming…)
Instead of two ellipses, suppose you are trying to cover the unit circle with three congruent ellipses. What is the smallest possible area one of these ellipses can have, such that they completely cover the circle? (If you are so inclined, then by all means look for N congruent ellipses, with N > 2.)
What is the smallest ellipse that will cover a third of circle?
This a bit easier two equilateral triangles from an inscribed hexagon in a circle nicely marks a third of a circle.
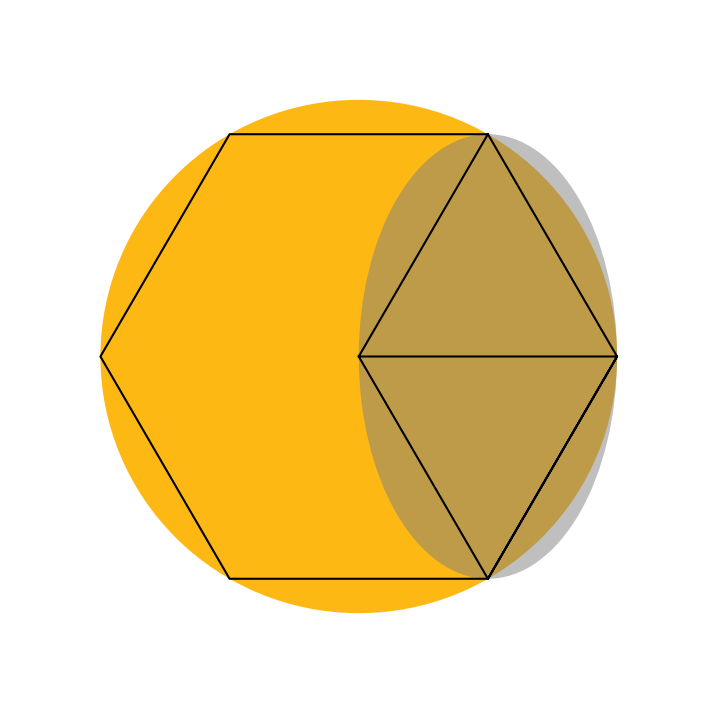
The minor axis is $1$ and the major axis $\sqrt{3}$.
The minor axis is horizontal from $(0, 0)$ to $(2a, 0)$.
The major axis is vertical from $(a, -b)$ to $(a, b)$.
The foci are at $(a, -\sqrt{-b^2-a^2})$ and $(a, \sqrt{-b^2-a^2})$.
Let $x_N = \cos{\frac{\pi}{N}}$ and $y_N = \sin{\frac{\pi}{N}}$.
$(0,0)$, $(x_N, y_N)$, and $(x_N, -y_N)$ bounds $\dfrac{1}{N}$ of a unit circle, so 1 ellipse should completely eclipse that portion of the sun.
$$2b = \sqrt{\left(a-x_N\right)^2 + (-\sqrt{-b^2-a^2}-y_N)^2} + \sqrt{\left(a-x_N\right)^2 + (\sqrt{b^2-a^2}-y_N)^2}$$
Substitute for the following,
$$B = y_N + \sqrt{b^2-a^2}$$
$$B_C = y_N - \sqrt{b^2-a^2}$$
$$2b = \sqrt{\left(a-x_N\right)^2 + B^2} + \sqrt{\left(a-x_N\right)^2 + {B_C}^2}$$
Squaring both sides,
$$4b^2 = B^2 + \left(a-x_N\right)^2 + 2\sqrt{\big(B^2+\left(a-x_N\right)^2\big) \cdot \big({B_C}^2+\left(a-x_N\right)^2\big)} + {B_C}^2 + \left(a-x_N\right)^2$$
$$4b^2 - B^2 - {B_C}^2 - 2\left(a-x_N\right)^2 = 2\sqrt{B^2{B_C}^2 + \left(a-x_N\right)^2\big(B^2 + {B_C}^2\big) + \left(a-x_N\right)^4}$$
$$\big(4b^2 - 2\left(a-x_N\right)^2 - (B^2 + {B_C}^2)\big)^2 = 4B^2{B_C}^2 + 4\left(a-x_N\right)^2\big(B^2 + {B_C}^2\big) + 4
2\left(a-x_N\right)^4$$
$$16b^4 - 16b^2\left(a-x_N\right)^2 + 4\left(a-x_N\right)^4 - 8b^2(B^2 + {B_C}^2) + 4\left(a-x_N\right)^2(B^2 + {B_C}^2) + (B^2 + {B_C}^2)^2 = 4B^2{B_C}^2 + 4\left(a-x_N\right)^2\big(B^2 + {B_C}^2\big) + 4\left(a-x_N\right)^4$$
$$16b^4 - 16b^2\left(a-x_N\right)^2 = 8b^2(B^2 + {B_C}^2) - (B^2 - {B_C}^2)^2$$
From above,
$$B^2 + {B_C}^2 = -2a^2 + 2b^2 +2{y_N}^2$$
$$B^2 - {B_C}^2 = 4{y_N}\sqrt{b^2-a^2}$$
Substituting,
$$16b^4 - 16b^2\left(a-x_N\right)^2 = 8b^2(-2a^2 + 2b^2 +2{y_N}^2) - (4{y_N}\sqrt{b^2-a^2})^2$$
$$16b^4 - 16b^2\left(a-x_N\right)^2 = 8b^2(-2a^2 + 2b^2 +2{y_N}^2) - (4{y_N}\sqrt{b^2-a^2})^2$$
$$b^4 - a^2b^2 + 2ab^2x_N - b^2{x_N}^2 = -a^2b^2 + b^4 +b^2{y_N}^2 + a^2{y_N}^2 - b^2{y_N}^2$$
$$ 2ab^2x_N - b^2{x_N}^2 = a^2{y_N}^2$$
$$b^2\bigg({\dfrac{2a}{x_N}-1}\bigg){x_N}^2= a^2({y_N}^2)$$
$$b = a \dfrac{y_N}{x_N}\sqrt{\dfrac{1}{\frac{2a}{x_N}-1}}$$
Substituing $\dfrac{y_N}{x_N} = \tan{\frac{\pi}{N}}$,
Substituting into $\pi ab$,
$$= \pi a^2\tan{\frac{\pi}{N}}\sqrt{\dfrac{x_N}{2a-x_N}}$$
$$= \pi \tan{\frac{\pi}{N}}\sqrt{x_N} \dfrac{a^2}{\sqrt{2a-x_N}}$$
Taking the derivative,
$$\dfrac{\big((2a-x_N)^{\frac{1}{2}} \cdot 2a\big) - \big(a^2 \cdot (2a-x_N)^{-\frac{1}{2}} \cdot \frac{1}{2} \cdot 2\big)}{2a-x_N} = 0$$
Multiplying by $\dfrac{(2a-x_N)^{\frac{1}{2}} }{(2a-x_N)^{\frac{1}{2}} }$,
$$\dfrac{4a^2-2a{x_N}- a^2}{(2a-x_N)^\frac{3}{2}} = 0$$
$$3a^2 = 2a{x_N}$$
Note that for $N = 4$ moons, $x_N = y_N = \dfrac{1}{\sqrt{2}}$. Thus, $a = \dfrac{\sqrt{2}}{3}$, the minor axis is less than one, and does not completely cover a quarter circle. $a= \frac{1}{2}$ and
$$b = \dfrac{1}{2}\sqrt{\dfrac{\frac{1}{\sqrt{2}}}{1-\frac{1}{\sqrt{2}}}}= \dfrac{1}{2}\sqrt{\dfrac{1}{\sqrt{2}-1}} = \dfrac{\sqrt{\sqrt{2}+1}}{2} \approx 0.777$$Note that for $N = 6$ moons, $a = b = \frac{2}{\sqrt{3}} \approx 0.577$. The moons are thus circles, and for $N ≥ 7$ the major axis is horizontal.
The major axis is horizontal from $(0, 0)$ to $(2b, 0)$.
The minor axis is vertical from $(b, -a)$ to $(b, a)$.
The foci are at $(b-\sqrt{-b^2-a^2}, 0)$ and $(b+\sqrt{-b^2-a^2}, 0)$.
Because ellipses and distance formulas have some symmetry,
The area of one ellipse is still
Note, for the sum of all the moon areas,
$$A_{\text{ALL}} = N \cdot \dfrac{2\pi}{\sqrt{27}} \cdot \sin{\frac{2\pi}{N}}$$
$$\lim\limits_{N\to\infty} N \cdot \sin{\dfrac{2\pi}{N}}$$
$$= 2\pi\lim\limits_{N\to\infty} \dfrac{N}{2\pi} \cdot \sin{\dfrac{2\pi}{N}}$$
$$= 2\pi\lim\limits_{N\to\infty} \dfrac{\sin{\dfrac{1}{N}}}{\dfrac{1}{N}}$$
Applying L'Hôpital's,
$$= 2\pi\lim\limits_{N\to\infty} \dfrac{\cos{\dfrac{1}{N}}\cdot-\dfrac{1}{N^2}}{-\dfrac{1}{N^2}}$$
$$= 2\pi\lim\limits_{N\to\infty} \cos{\dfrac{1}{N}} = 2\pi$$
Thus,
Take a peek!