Can You Paint by Number?

Fiddler

I’m completing a paint-by-number painting, although this one is a little different from any that I’ve seen before. It’s an infinitely long strip of canvas that is 1 cm wide. It’s broken up into adjacent 1 cm-by-1 cm squares, each of which is numbered zero or one, each with a 50 percent chance. The squares are all numbered independently of each other. Every square with a zero I color red, while every square with a one I color blue.

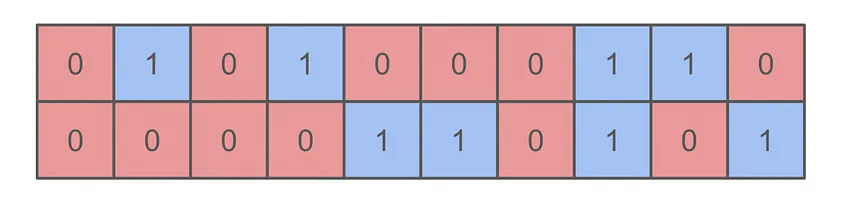
Once I’m done painting, there will be many “clusters” of contiguous red and blue squares. For example, consider the finite strip of canvas below. It contains 10 total squares and seven clusters, which means the average size of a cluster here is approximately 1.43 squares.

Once I’m done painting, what will be the average size of each red or blue cluster?

Solution

Let $X_s$ represent the average number of clusters for a strip of length $s$. I will use induction to show that:

$$X_s = \dfrac{s+1}{2}$$

$s = 1$:

There are only two possibilities. A single red square or a single bue square. The average number of clusters is

$$X_1 = \dfrac{1+1}{2} = 1$$

$s = k-1$:

Assume

$$X_{k-1} = \dfrac{k-1+1}{2} = \dfrac{k}{2}$$

$s = k$:

For $s = k-1$, there are $2^{k-1}$ possible strips. The average number of clusters for those strips is $\dfrac{k}{2}$.

• Half the time the next square added will match the last square of $X_{k-1}$. They will have no new clusters.
• Half the time the next square added will be different from the last square of $X_{k-1}$. They will have one new cluster.

$$X_k = \dfrac{k}{2} + \dfrac{1}{2} \cdot 1 = \dfrac{k + 1}{2}$$

Answer

Since there are $s$ squares and an average of $\frac{s + 1}{2}$ clusters, the average cluster size is :

$$\dfrac{s}{\frac{s + 1}{2}}$$

$$= \dfrac{2s}{s + 1} \approx 2$$

Extra Credit

Once again, I’m painting an infinitely long strip of canvas, broken up into adjacent 1 cm-by-1 cm squares. Squares are randomly and independently numbered 0 or 1 as before. But this time, the strip itself is 2 cm wide.

Squares are considered adjacent if they share a common edge. So squares can be horizontally or vertically adjacent, but not diagonally adjacent.

Once I’m done painting, there will again be many “clusters” of contiguous red and blue squares. The example below contains 20 total squares and nine clusters, which means the average size of a cluster here is approximately 2.22 squares.

Once I’m done painting, what will be the average size of each red or blue cluster?

Solution

Let $Y_s$ represent the average number of clusters for a strip of length $s$. I will use induction to show that:

$$Y_s = \dfrac{5s+7}{8}$$

$s = 1$:

There are only four possibilities:

• Two red squares - 1 cluster.
• One red square, one blue square - 2 clusters.
• One blue square, one red square - 2 clusters.
• Two blue squares - 1 cluster.

The average number of clusters agrees with:

$$Y_1 = \dfrac{5+7}{8} = \dfrac{3}{2}$$

$s = k-1$:

Assume

$$Y_{k-1} = \dfrac{5(k-1)+7}{8}$$

$s = k$:

For $s = k-1$, there are $\left(2^{k-1}\right)^2 = 2^{2k-2}$ possible strips. The average number of clusters for those strips is $\dfrac{5(k-1)+7}{8}$.

Similar to what was done in the Fiddler, compare the two new squares to the last two previous squares to determine how many new clusters are added. The following table summarizes the 16 possibilities into 6 groups.

Last Two Squares of $Y_{k-1}$	Last Two Squares of $Y_k$	Probability	Number of New Clusters
$RR$ or $BB$	Same as $Y_{k-1}$	$\dfrac{1}{8}$	0
$RR$ or $BB$	Opposite of $Y_{k-1}$	$\dfrac{1}{8}$	1
$RR$ or $BB$	$RB$ or $BR$	$\dfrac{1}{4}$	1
$RB$ or $BR$	$RR$ or $BB$	$\dfrac{1}{4}$	0
$RB$ or $BR$	Same as $Y_{k-1}$	$\dfrac{1}{8}$	0
$RB$ or $BR$	Opposite of $Y_{k-1}$	$\dfrac{1}{8}$	2

For $s = k$, there are $2^{2k}$ possible strips. From the table above,

• $\frac{1}{2}$ of the strips have the same number of clusters.
• $\frac{3}{8}$ of the strips have 1 more cluster.
• $\frac{1}{8}$ of the strips have 2 more clusters.

$$Y_k = \dfrac{5(k-1)+7}{8} + \dfrac{3}{8} \cdot 1 + \dfrac{1}{8} \cdot 2$$

$$= \dfrac{5k+7}{8}$$

Answer

Since there are $2s$ squares and an average of $\frac{5s+7}{8}$ clusters, the average cluster size is :

$$\dfrac{2s}{\frac{5s+7}{8}}$$

$$= \dfrac{16s}{5s+7} \approx \dfrac{16}{5}$$

Rohan Lewis

2024.04.07