Can You Pour the Water?¶

Fiddler¶

Last weekend, I saw an old friend of mine (in fact, he was the composer of an opera I performed in several decades ago!) who recently subscribed to The Fiddler. He confessed that the last time he encountered math puzzles like these, they were water pouring puzzles. “Oh, I can do one of those!,” I exclaimed.

So Joel, this week’s puzzle is dedicated to you!

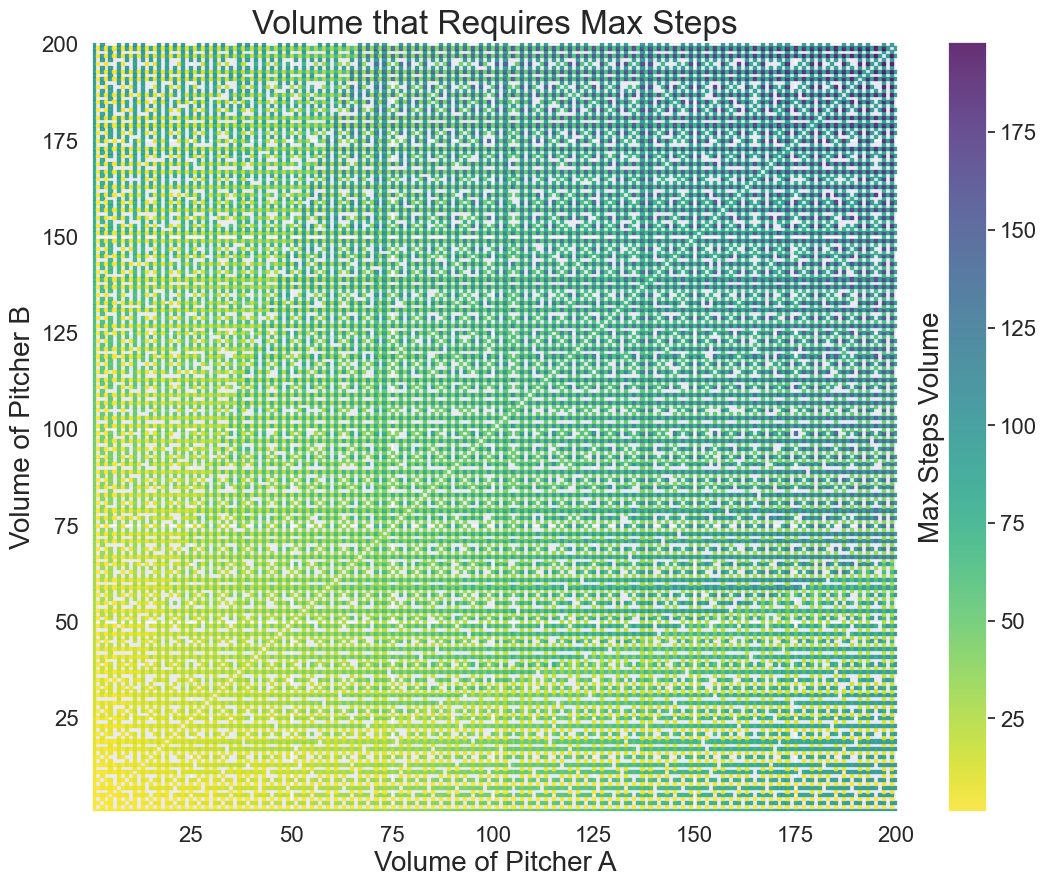
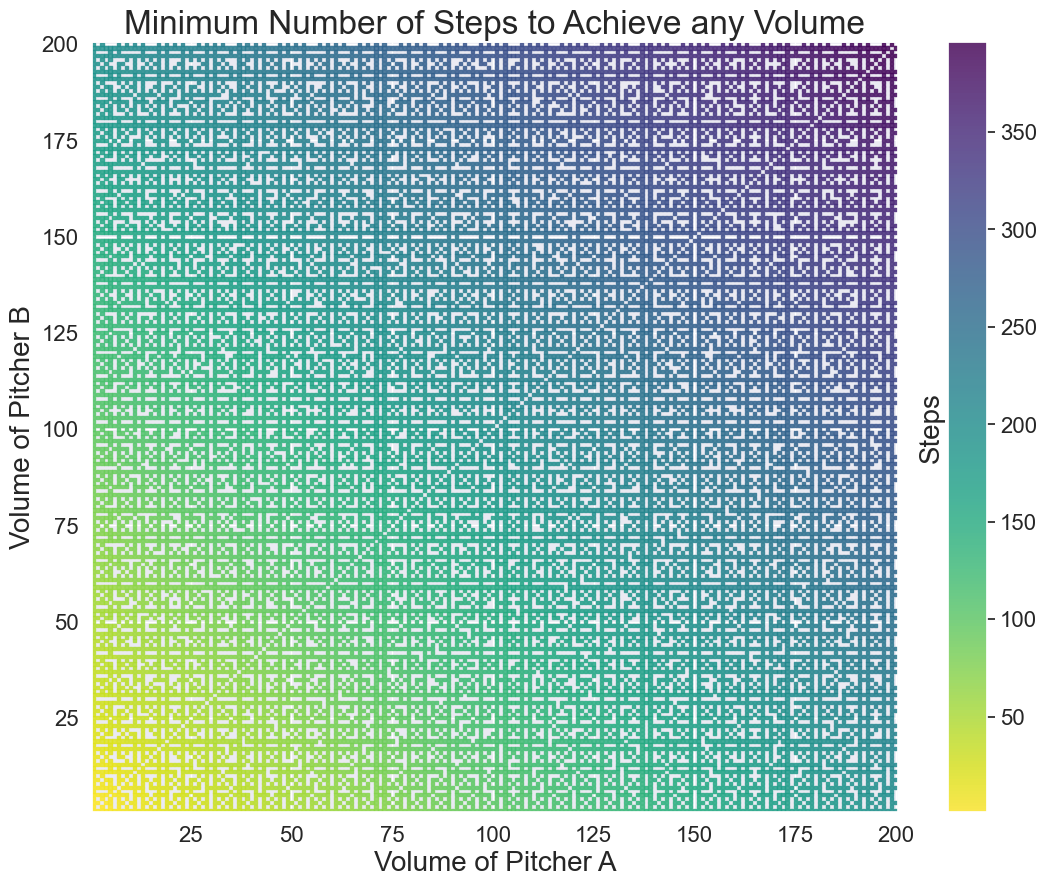
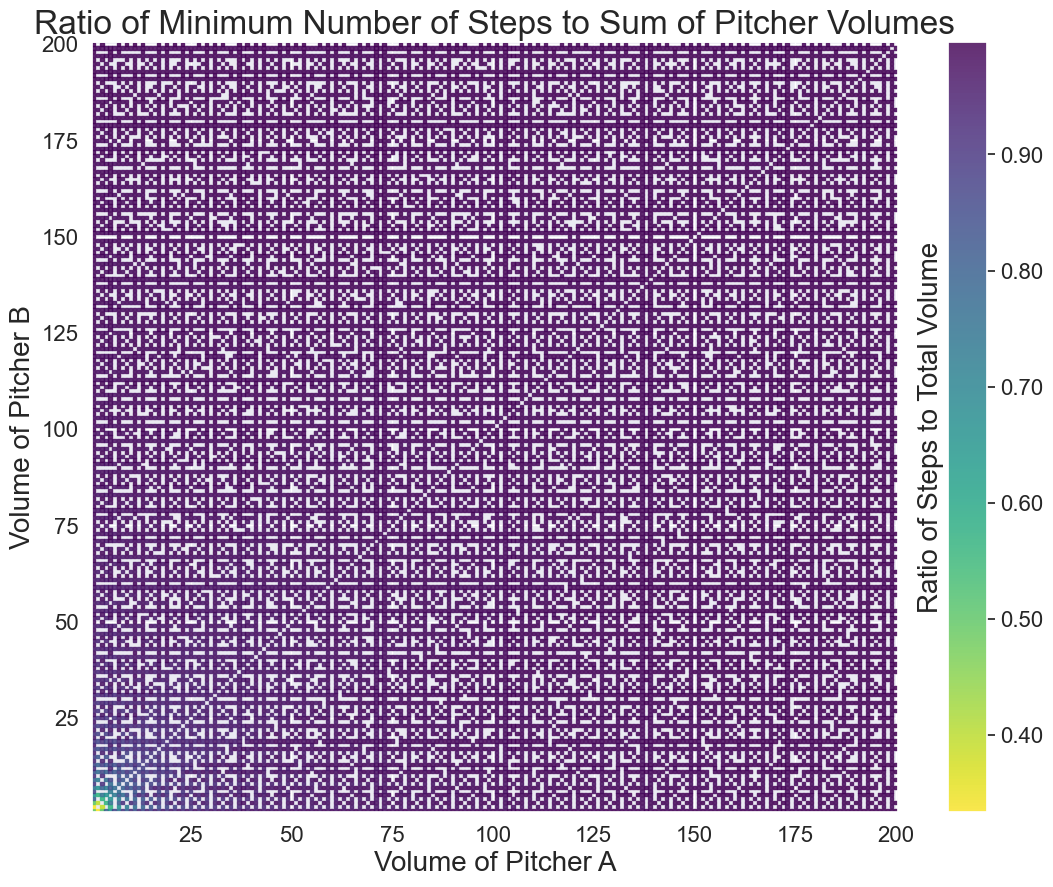
I have two large pitchers with known volumes: 10 liters (“pitcher A”) and 3 liters (“pitcher B”). They are both initially empty. I can do one of six things with the pitchers:

  1. I can fill pitcher A to the top with water from the sink.

  2. I can fill pitcher B to the top with water from the sink.

  3. I can empty the contents of pitcher A into the sink.

  4. I can empty the contents of pitcher B into the sink.

  5. I can transfer the contents of pitcher A to pitcher B, until pitcher A is empty or pitcher B is filled to the top—whichever comes first.

  6. I can transfer the contents of pitcher B to pitcher A, until pitcher B is empty or pitcher A is filled to the top—whichever comes first.

Every time I do any one of the above six, it counts as a step.

What is the fewest number of steps required until one of the pitchers (either A or B) contains precisely 5 liters of water?

Solution¶

Step Pitcher Action Volume of A Volume of B
1 Fill B. 0 3
2 Empty B into A. 3 0
3 Fill B. 3 3
4 Empty B into A. 6 0
5 Fill B. 6 3
6 Empty B into A. 9 0
7 Fill B. 9 3
8 Fill A with 1 liter from B. 10 2
9 Empty A. 0 2
10 Empty B into A. 2 0
11 Fill B. 2 3
12 Empty B into A. 5 0

To be sure, I checked starting with A.

Step Pitcher Action Volume of A Volume of B
1 Fill A. 10 0
2 Fill B from A. 7 3
3 Empty B. 7 3
4 Fill B from A. 4 3
5 Empty B. 4 0
6 Fill B from A. 1 3
7 Empty B. 1 0
8 Fill B with 1 liter from A. 0 1
9 Fill A. 10 1
10 Fill B with 2 liters from A. 8 3
11 Empty B. 8 0
12 Fill B from A. 5 3

Answer¶

Achieving 5 liters takes a minimum of 12 steps. This can be done in two ways.

Extra Credit¶

Instead of 10 liters and 3 liters, suppose the volumes of the pitchers A and B are now 100 liters and 93 liters, respectively.

Further suppose that the fewest number of steps needed until one of the pitchers (either A or B) contains precisely N liters of water is f(N), where N is a whole number between 1 and 100, inclusive.

What is the maximum value of f(N), and for which value of N does this occur?

Solution¶

I created code that did the following :

  1. Start with :
    1. Step number.
      • Initialize with 0 steps.
    2. An $(a+1) \text{ x } (b+1)$ matrix
      • A state is the ordered pair $(a,b)$, where $a$ and $b$ are the represent the amount of water in pitchers A and B.
      • The array is to check if a state has existed already, and the minimum number of steps to get there.
      • Initialize with $[0,0] = 0$ in the array. The rest are NA.
    3. A list of states
      • Initialize state $[0,0]$.
      4. .
  2. Begin
  3. Create an empty list of new states
  4. Increase the step number by 1.
  5. For each state in the list of states, check and see if applying any of the following options to it (the next state) has already been visited in the array of states:
    • Does filling A create a new state?
    • Does filling B create a new state?
    • Does emptying A create a new state?
    • Does emptying B create a new state?
    • If the amount in A $<$ empty amount in B, does emptying A into B create a new state?
    • If the amount in A $≥$ empty amount in B, does filling B from A create a new state?
    • If the amount in B $<$ empty amount in A, does emptying B into A create a new state?
    • If the amount in B $≥$ empty amount in A, does filling A from B create a new state?
  6. Once all old states have been checked, look at new states.
    • If there is at least one new state, repeat from Begin.
    • If there are no new states, the array is complete.
  7. Getting the steps for each volume:
    • If the steps $>$ B, check for the minimum value in row $a$.
    • If the steps $≤$ B, check for the minimum of the minimum value in row $a$ and the minimum value in column $b$.
    • The maximum of all the minimums can be easily found.

I used a breadth first search as it guarantees that the array is populated by the minimum number of steps or not at all.

Answer¶

Achieving 50 liters takes 190 steps.

I plotted my results of all pitcher sizes from 1 to 200 liters.

If the $gcd(a,b) ≠ 1$, they were removed, as not all pitcher sizes would be possible for that pair.

The volume that requires the maximum number of steps is exactly half of the larger of the two pitchers if the larger is even. This is observable at the blocks of the same color in any even row or column.

I could not determine any immediate pattern if the larger pitcher is odd.

The steps required to achieve that volume is also plotted.

This seems to be directly proportional to the size of the pitchers, so I graphed a ratio, $r = \dfrac{\text{Number of Steps}}{\text{Volume of A and B}}$ .

Rohan Lewis¶

2024.04.01¶

Code can be found here.