Can You Fairly Cut the Birthday Cake?

Fiddler

For all those special people who have birthdays this month, here’s a fun geometry puzzle from Friend-of-The-Fiddler Dean Ballard:

You and two friends all have March birthdays, so you’ve decided to celebrate together with one big cake that has delicious frosting around its perimeter. To share the cake fairly, you want to ensure that (1) each of you gets the same amount of cake, by area, and (2) each of you gets the same amount of frosting along the cake’s edge.

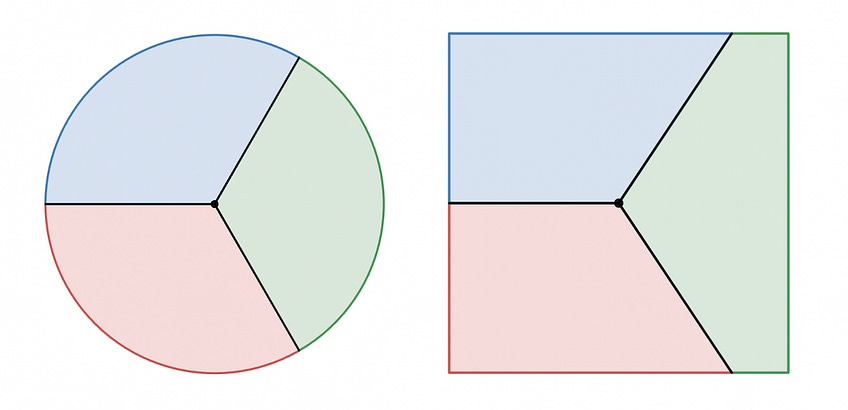
What’s more, you want to cut the cake by starting at a single point inside of it, and then making three straight cuts to the edge from that point. You’ve already worked out ways to do this for circular and square cakes, as shown below.

</div>

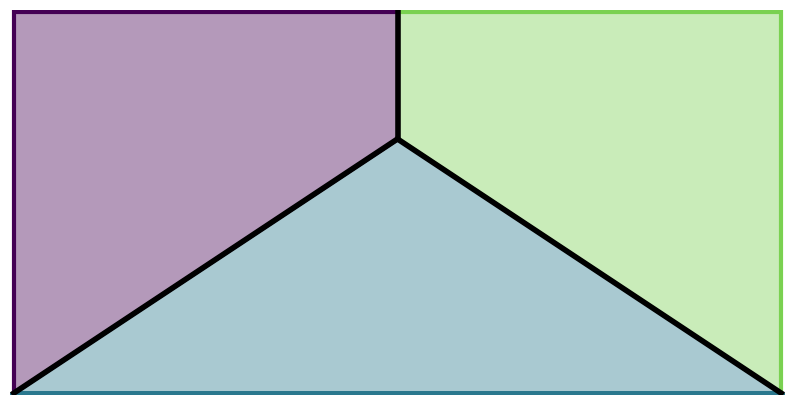
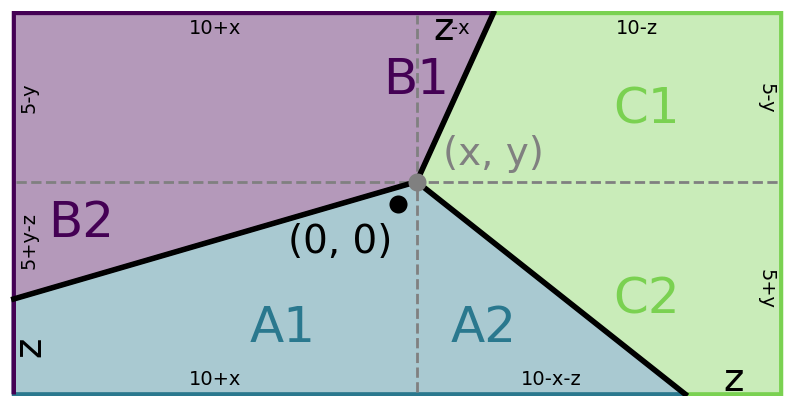
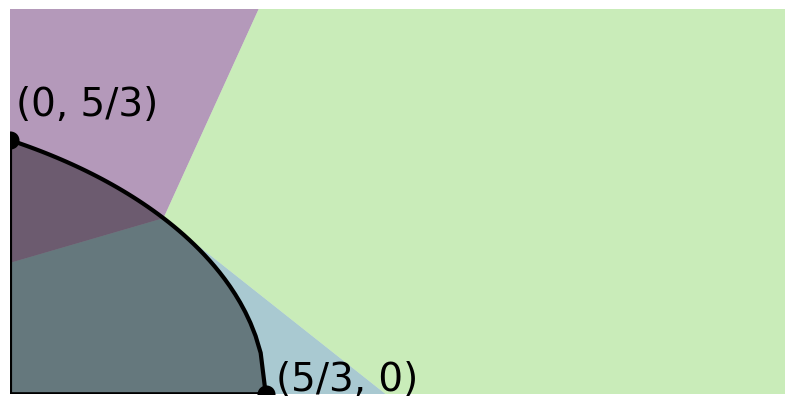
However, the cake you bought is rectangular, with a length of 20 inches and a width of 10 inches. Using the coordinate system of your choice, describe a way this particular cake can be cut fairly, so that all three of you get the same amount in terms of both area and the cake’s perimeter. Again, there should be three straight cuts emanating from a single point inside the cake.

To be clear, the three pieces themselves need not have the same perimeter. Instead, each piece must have the same amount of the perimeter from original, uncut cake.

Solution

Center the cake about the origin and orient it horizontally. Let the corners be:

• $(-10, -5)$
• $(-10, 5)$
• $(10, 5)$
• $(10, -5)$

We know the perimeter is $60 \text{ in}$ so each friend will receive $20 \text{ in}^2$ The area is $200 \text{ in}^2$ so each friend will receive $\frac{200}{3} \text{ in}^2$ of the cake.

I came up with two answers simultaneously.

One player receives an entire $20\text{ in}$, side of frosting. The other two equally receive $10 \text{ in}^2$ and $10 \text{ in}$, and a corner.

Since there is horizontal symmetry, $x = 0$.

Solving for the area of the triangle,

$$A = \frac{1}{2} \cdot b \cdot h$$$$\dfrac{200}{3} = \frac{1}{2} \cdot 20 \cdot (5+y)$$$$\dfrac{20}{3} = 5+y$$$$y = \dfrac{5}{3}$$

One player receives the entire $10 \text{ in}$ short side of frosting and equal $10 \text{ in}$ frostings from the adjacent sides. The other two receive $15 \text{ in}^2$ and $5 \text{ in}$, and a corner.

Since there is now vertical symmetry, $y = 0$

Solving for the area of the trapezoid,

$$A = \frac{a+b}{2} \cdot h$$$$\dfrac{200}{3} = \frac{15 + (10+x)}{2} \cdot 5$$$$\dfrac{80}{3} = 25+x$$$$x = \dfrac{5}{3}$$

Answers

The three slices could meet at $\left(0, \frac{5}{3}\right)$ or $\left(\frac{5}{3}, 0\right)$.

Extra Credit

By now, you’ve hopefully found at least one central point from which you can make your three straight cuts, so that you and your two friends each get the same amount of birthday cake, in terms of both area and the frosting along the edge.

As it turns out, there are many possible central points from which you can fairly cut the 20-inch by 10-inch rectangular cake. Together, these points form a locus that’s a closed shape.

For Extra Credit, what is the area contained within this shape?

Solution

This diagram starts with my first answer from Fiddler and shifts each friends' frosting perimeter $z \text{ in}$ clockwise.

The slices meet at some point $(x,y)$ away from the origin in the first quadrant, because the path of the point of concurrency is moving in some path from $\left(0, \frac{5}{3}\right)$ to $\left(\frac{5}{3}, 0\right)$.

Solving for the area of the bottom quadrilateral:

$$\text{Area} \text{ }=\text{ } A_1 + A_2 \text{ }=\text{ } \dfrac{a_1+b_1}{2} \cdot h_1 \text{ }+\text{ } \frac{1}{2} \cdot b_2 \cdot h_2$$$$\dfrac{200}{3} \text{ } = \text{ } \dfrac{z+(5+y)}{2} \cdot (10+x) \text{ }+\text{ } \frac{1}{2} \cdot (5+y) \cdot (10-x-z)$$$$400 \text{ } = \text{ } 3\big((y+z+5) \cdot (x+10) \text{ }+\text{ } (y+5)\cdot (-x-z+10)\big)$$$$400 \text{ } = \text{ } 3\big(xy+10y+xz+10z+5x+50) + (-xy-yz+10y-5x-5z+50)\big)$$$$400 \text{ } = \text{ } 3\big(xz-yz+20y+5z+100\big)$$

$0 = 3xz-3yz+60y+15z-100$

Solving for the area of the top left quadrilateral:

$$\text{Area} \text{ }=\text{ } B_1 + B_2 \text{ }=\text{ } \dfrac{a_1+b_1}{2} \cdot h_1 \text{ }+\text{ } \frac{1}{2} \cdot b_2 \cdot h_2$$$$\dfrac{200}{3} \text{ } = \text{ } \dfrac{(10+x+z-x)+(10+x)}{2} \cdot (5-y) \text{ }+\text{ } \frac{1}{2} \cdot (10+x) \cdot (5+y-z)$$$$400 \text{ } = \text{ } 3\big((x+z+20) \cdot (-y+5) \text{ }+\text{ } (x+10)\cdot (y-z+5)\big)$$$$400 \text{ } = \text{ } 3\big(-xy+5x-yz+5z-20y+100) + (xy-xz+5x+10y-10z+50)\big)$$$$400 \text{ } = \text{ } 3\big(-xz-yz+10x-10y-5z-20y+150\big)$$

$0 = 3xz+3yz-30x+30y+15z-50$

Solving for the area of the right side quadrilateral:

$$\text{Area} \text{ }=\text{ } C_1 + C_2 \text{ }=\text{ } \dfrac{a_1+b_1}{2} \cdot h_1 \text{ }+\text{ } \dfrac{a_2+b_2}{2} \cdot h_2$$$$\dfrac{200}{3} \text{ } = \text{ } \dfrac{(10-z)+(10-x)}{2} \cdot (-y+5) \text{ }+\text{ } \dfrac{(10-x) + z}{2} \cdot (y+5)$$$$400 \text{ } = \text{ } 3\big((-x-z+20) \cdot (-y+5) \text{ }+\text{ } (-x+z+10)\cdot (y+5)\big)$$$$400 \text{ } = \text{ } 3\big(xy-5x+yz-5z-20y+100) + (-xy-5x+yz+5z+10y+50)\big)$$$$400 \text{ } = \text{ } 3\big(2yz-10x-10y+150\big)$$

$0 = 6yz-30x-30y+50$

Solve $0 = 3xz-3yz+60y+15z-100$ and $0 = 6yz-30x-30y+50$ for $z$:

$$0 = 3xz-3yz+60y+15z-100$$ $$3xz-3yz+15z = 100-60y$$ $$z = \dfrac{100-60y}{3x-3y+15}$$

$$0 = 6yz-30x-30y+50$$ $$6yz=30x+30y-50$$ $$z = \dfrac{30x+30y-50}{6y}$$

Setting equal to each other $$\dfrac{100-60y}{3x-3y+15}= \dfrac{30x+30y-50}{6y}$$ $$\dfrac{10-6y}{x-y+5}= \dfrac{3x+3y-5}{2y}$$ $$20y-12y^2= 3x^2+3xy-5x-3xy-3y^2+5y+15x+15y-25$$ $$9y^2 = -3x^2-10x+25$$

$y = \pm\dfrac{\sqrt{(-3x+5)(x+5)}}{3}$
Note that $\left(0, \frac{5}{3}\right)$ and $\left(\frac{5}{3}, 0\right)$ are solutions.

$$A =\int\limits_0^{5/3} \frac{1}{3}\sqrt{-3x^2+10x-25}dx$$

Using a solver,

$$A = \dfrac{900\pi -25\cdot \sqrt{3^7}}{2\cdot \sqrt{3^{11}}} \approx 1.970 \text{ in}^2$$

Answer

The region bounded by $9y^2 = 3x^2+10x-25$ has an Area of $4*1.970 \approx 7.88 \text{ in}^2$.

Here are the cuts happening.

In order to produce the visual above, $x$ and $y$ were determined parametrically from $z$.

Solve $0 = 3xz-3yz+60y+15z-100$ and $0 = 6yz-30x-30y+50$ for $y$ this time:

$$0 = 3xz-3yz+60y+15z-100$$ $$3yz-60y = 3xz+15z-100$$ $$z = \dfrac{3xz+15z-100}{3z-60}$$

$$0 = 6yz-30x-30y+50$$ $$6yz-30y = 30x-50$$ $$z = \dfrac{30x-50}{6z-30}$$

Setting equal to each other $$\dfrac{3xz+15z-100}{3z-60}= \dfrac{30x-50}{6z-30}$$ $$\dfrac{3xz+15z-100}{z-20}= \dfrac{15x-25}{z-5}$$ $$3xz^2 + 15z^2 - 100z - 15xz - 75z + 500 = 15xz - 25z - 300x + 500$$ $$3xz^2 - 30xz + 300x = -15z^2+150z$$ $$x = \dfrac{-5z^2+50z}{z^2 - 10z + 100}$$

Rohan Lewis

2024.03.04

Code can be found here.