From Nis Jørgensen comes a pernicious puzzle of pancakes:
Three siblings are at a playground: Alice, Bob, and Carey. Alice, the oldest, gets a call from their dad—their pancake dinner is ready! But they won’t get to eat until all three kids are home.
They each walk home at a different constant speed. Alice can walk home in 10 minutes, Bob can do it in 20, and Carey in 30. Fortunately, any of the kids can carry any of the others on their back without reducing their own walking speed. (However, none of them can carry a kid who is, in turn, carrying another kid.) Assume that they can pick someone up, set someone down, and change direction instantaneously.
What is the fastest they can all get home? (Your answer should be in minutes.)
At any point in the procedure, the average speed of everyone walking towards home should be as fast as possible. This means given $s$ siblings, the slowest $\lfloor {\dfrac{s}{2}} \rfloor$ should be on some else's back.
The distance between Alice and Bob is currently $\frac{1}{2}$ the distance to home. Since Alice is twice as fast as Bob, Alice will walk $\frac{2}{3} \cdot \frac{1}{2} = \frac{1}{3}$ and Bob will walk $\frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}$. $\frac{1}{3}$ of $10$ min is $3 \frac{1}{3}$ min.
Alice takes the same amount of time on the return trip.
Nis Jørgensen also offered the following Extra Credit:
Suppose Alice, Bob, and Carey have a fourth sibling named Dee, who is with them at the playground. Dee is the slowest, needing 60 minutes to walk home. As before, any kid can carry any other kid, and they won’t start eating until everyone is home.
Once again, what is the fastest they can all get home? (Your answer should be in minutes.)
Using the same optimization principle as above...
Same as before, Alice will walk back. $\frac{1}{3}$ of $10$ min is $3 \frac{1}{3}$ min.
Dee now jumps on to Alice.
The distance between Alice and Bob is currently $\frac{1}{6}$ the distance to home. Since Alice is twice as fast as Bob, Alice will walk $\frac{2}{3} \cdot \frac{1}{6} = \frac{1}{9}$ and Bob will walk $\frac{1}{3} \cdot \frac{1}{6} = \frac{1}{18}$. $\frac{1}{9}$ of $10$ min is $1 \frac{1}{9}$ min.
Same as before, Alice takes the same amount of time on the return trip.
They can all arrive home by $18 \dfrac{8}{9}$ min. The graph below visualizes the trips.
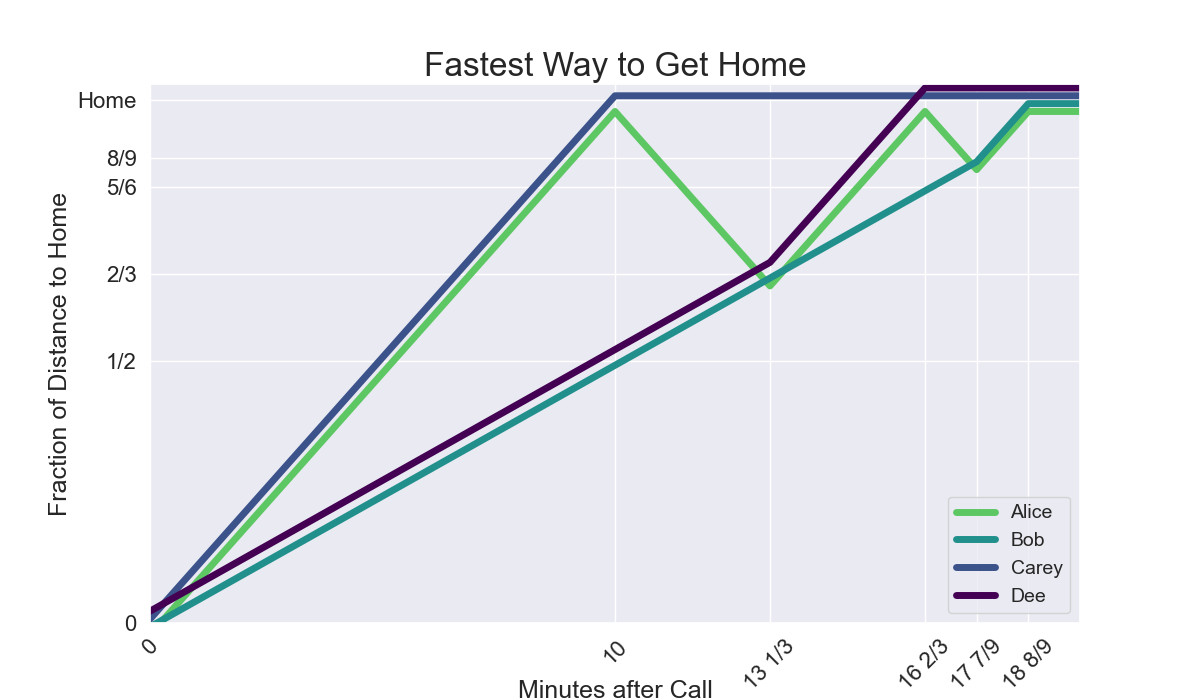
Note that since neither Carey nor Dee walk, they can be switched in this problem to yield a different solution with the same end result.