Can You Flip the Coins Exactly as You’d Expect??

Fiddler

From Raven Deerwater comes a metapuzzle of coin flipping:

If you flip three (independent) fair coins, there are four possible outcomes:

• You can get three heads, with a probability of 1/8.

• You can get two heads, with a probability of 3/8.

• You can get one heads, with a probability of 3/8.

• You can get zero heads, with a probability of 1/8.

Now suppose you are flipping three coins, and you do this eight times. What is the probability that you’ll get exactly one occurrence of three heads, three occurrences of two heads, three occurrences of one heads, and one occurrence of zero heads? (Note that these eight occurrences can happen in any order.)

Solution

• $P(\text{3 heads, 1 occurence}) = \left(\dfrac{1}{8}\right)^1$.
• $P(\text{2 heads, 3 occurences}) = \left(\dfrac{3}{8}\right)^3$.
• $P(\text{1 heads, 3 occurences}) = \left(\dfrac{3}{8}\right)^3$.
• $P(\text{0 heads, 1 occurence}) = \left(\dfrac{1}{8}\right)^1$.
• Number of ways to order 8 triple rolls = $\dfrac{8!}{1!3!3!1!}$

Answer

$$\left(\dfrac{1}{8}\right)^1 \left(\dfrac{3}{8}\right)^3 \left(\dfrac{3}{8}\right)^3 \left(\dfrac{1}{8}\right)^1 \cdot \dfrac{8!}{1!3!3!1!}$$

$$= \dfrac{3^6 \cdot 5 \cdot 7}{2^{19}} = \dfrac{25515}{524288} \approx 4.867\%$$

Extra Credit

Again, suppose you are flipping three fair and independent coins, and you do this eight times. Among the four possible outcomes (three heads, two heads, one heads, zero heads), the outcome that happens to occur most frequently—but, importantly, I’m not saying which one this is!—occurs a times. The next most frequent outcome occurs b times. The next most frequent after that occurs c times. And the least frequent occurs d times. Note that a+b+c+d = 8, and that a ≥ b ≥ c ≥ d. (Yes, equalities are allowed here).

Which ordered quadruple (a, b, c, d) is most likely?

Solution

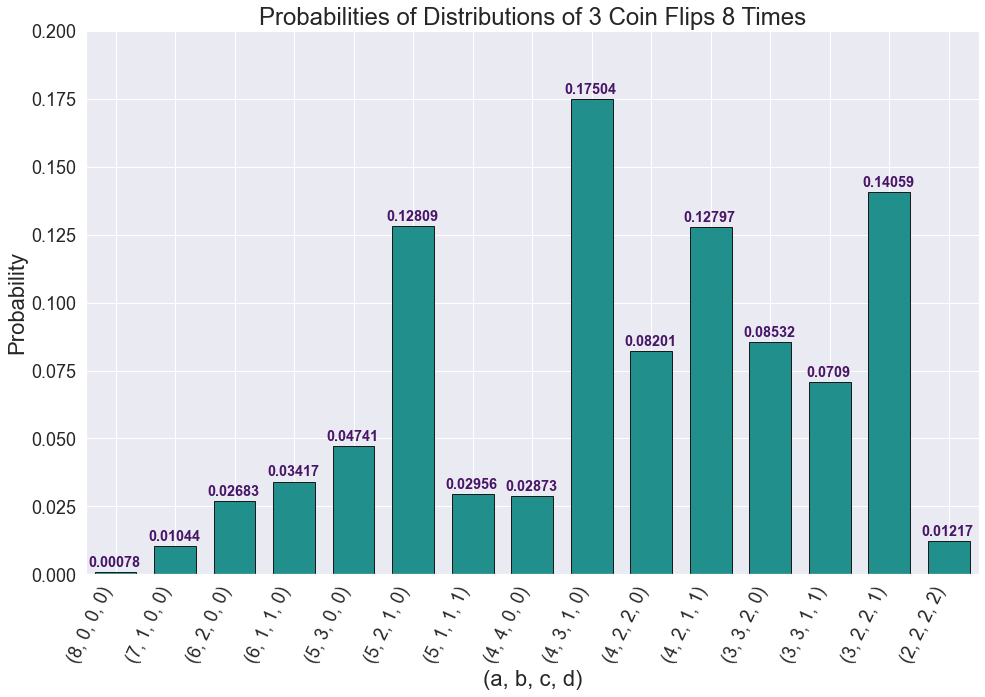
There are 15 ordered quadruples of $(a,b,c,d)$:

1. $(8, 0, 0, 0)$
2. $(7, 1, 0, 0)$
3. $(6, 2, 0, 0)$
4. $(6, 1, 1, 0)$
5. $(5, 3, 0, 0)$
6. $(5, 2, 1, 0)$
7. $(5, 1, 1, 1)$
8. $(4, 4, 0, 0)$
9. $(4, 3, 1, 0)$
10. $(4, 2, 2, 0)$
11. $(4, 2, 1, 1)$
12. $(3, 3, 2, 0)$
13. $(3, 3, 1, 1)$
14. $(3, 2, 2, 1)$
15. $(2, 2, 2, 2)$

I then ran code on each ordered quadruple:

• I calculated the probability 24 times, as there are $4!$ ways to order the four roll types.


• I then divided by the number of ways of overcounting, here are some examples
  :
  • $(8, 0, 0, 0)$ has only $4$ ways, so the probability was divided by $6$.
  • $(5, 2, 1, 0)$ has all $24$ ways, so the probability was divided by $1$.
  • $(4, 4, 0, 0)$ has all $6$ ways, so the probability was divided by $4$.
  • $(2, 2, 2, 2)$ has only $1$ way, so the probability was divided by $24$.

The plot below summarizes the findings:

Answer

$(4, 3, 1, 0)$ is most likely, occuring about $17.5\%$ of the time.

Rohan Lewis

2023.11.17

Code can be found here.