Answer¶
Two trapezoids yields a combined area of $6\cdot\dfrac{\sqrt{3}}{4}r^2$
$\dfrac{6\cdot\frac{\sqrt{3}}{4}}{\pi} \approx 82.70\%$ of the circle.
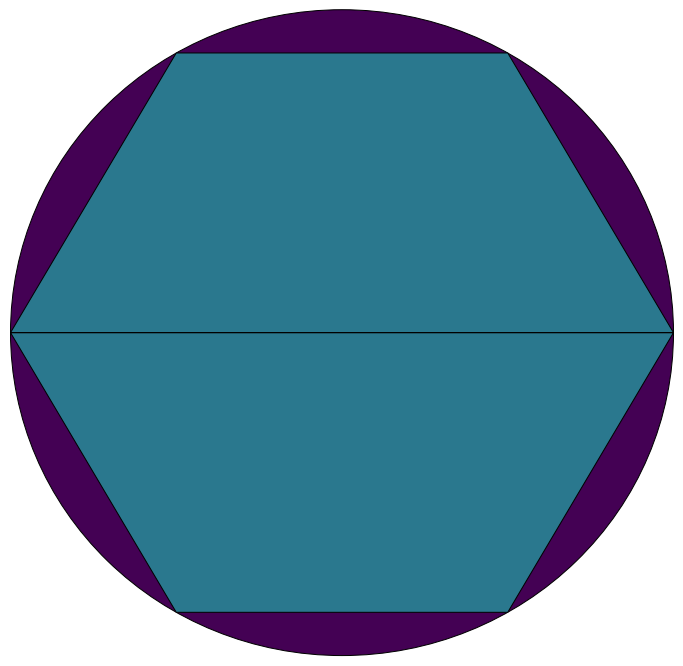
Your goal is to squeeze two non-overlapping quadrilaterals within a unit circle (i.e., a circle with radius 1). The quadrilaterals can share common edges, parts of edges, or vertices, but their interiors may not overlap. Their vertices may also lie on the circle’s circumference.
What is the greatest combined area these quadrilaterals can have? The quadrilaterals must be convex or concave (or one of each), but “crossed” or “bowtie” quadrilaterals are not allowed here.
In order to maximize the area, there must be a maximum number of circular segments.
Two trapezoids yields a combined area of $6\cdot\dfrac{\sqrt{3}}{4}r^2$
$\dfrac{6\cdot\frac{\sqrt{3}}{4}}{\pi} \approx 82.70\%$ of the circle.

From Jason Zimba comes (in my humble opinion) a trickier puzzle of polygons inscribed within circles:
For any four distinct points on a unit circle, define Z as the following sum: the area of the (convex) quadrilateral formed by all four of these points plus the area of the largest triangle (by area) formed by any three of these points.
For example, if the four points were the vertices of an inscribed square, then Z would equal 2—the area of the square—plus 1—the area of the largest triangle formed by three of the points (in this case, the area of any of them)—for a total value of 3.
Given that the four distinct points can be anywhere on the unit circle, what is the greatest possible value of Z?
(Note for all graphics below, part of the quadrilateral is completely 'under' the triangle.)
Since a quadrilateral and triangle are being inscribed in a circle, symmetry can be assumed.
The given information gave the maximum area of the quadrilateral, a square with area $2$, and the corresponding triangle with area $1$.
$\dfrac{2+1}{\pi} \approx 95.49\%$ of the circle.

Similarly the maximum area of the triangle, an equilateral triangle with area $\dfrac{3\sqrt{3}}{4}$, and the corresponding quadrilateral with area $\sqrt{3}$.
$\dfrac{\dfrac{3\sqrt{3}}{4}+\sqrt{3}}{\pi} \approx 96.48\%$ of the circle.

Create a variable $a$ to solve for the maximum, which is likely going to occur the above two cases.
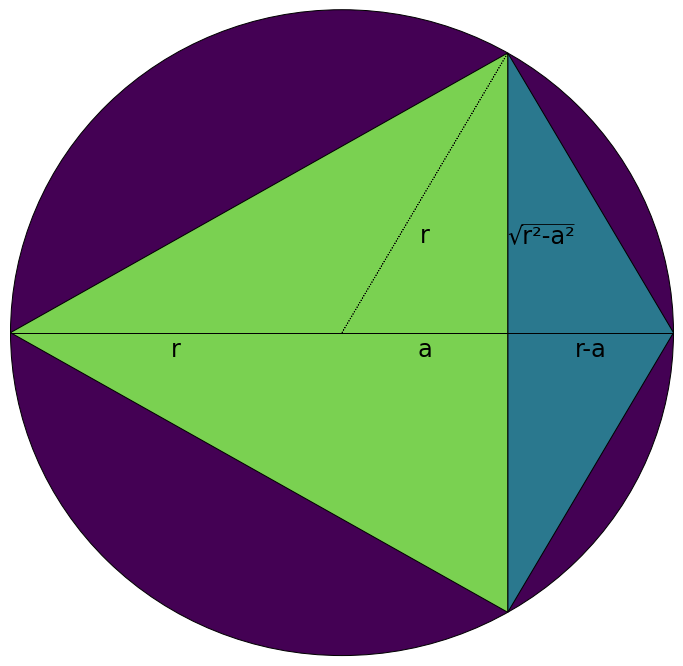
$$Triangle = \dfrac{1}{2} \cdot (r+a) \cdot 2\sqrt{r^2-a^2} = (r+a)\sqrt{r^2-a^2}$$
$$Total = (3r+a)\sqrt{r^2-a^2}$$
Taking the derivative to determine the maximum,
$$0 = \dfrac{(3r+a)}{\sqrt{r^2-a^2}}\cdot \frac{1}{2} \cdot (-2a) + \sqrt{r^2-a^2}$$
$$0 = -3ar-a^2 + r^2 - a^2$$
$$0 = 2a^2 +3ar - r^2$$
Using the quadratic formula,
$$a = \dfrac{-3r \pm \sqrt{9r^2 + 8r^2}}{4}$$
$$a = \dfrac{\sqrt{17}-3}{4}r \approx 0.2808r$$
Substituting $a$ into the total area expression above,
$\dfrac{\left(9+\sqrt{17}\right)\sqrt{6\sqrt{17}-10}}{\pi} \approx 100.23\%$ of the circle.