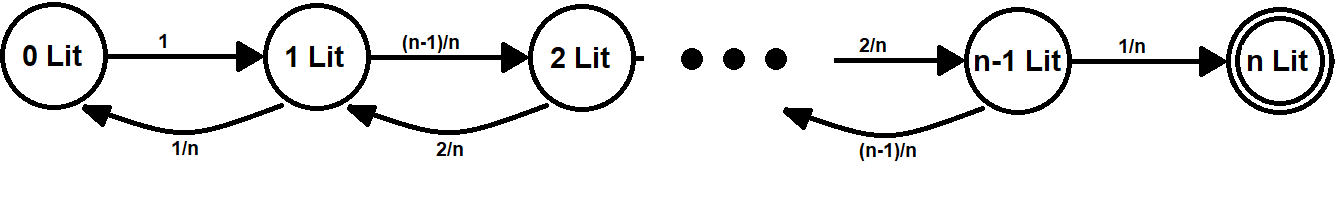L = 2¶
The following Markov model represents two lanes in this pinball game.
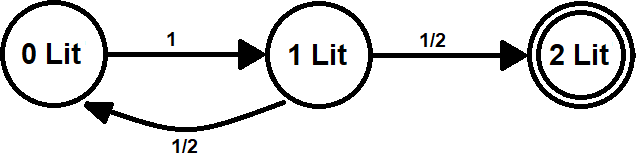
Let $t_k$ represent the number of flips it takes from $k$ lit lanes to get to 2 lit lanes.
$t_2 = 0$
$t_1 = 1 + \dfrac{1}{2}t_0 + \dfrac{1}{2}t_2$
$t_0 = 1 + t_1$
Solving yields
$$t_0 = E(2) = 4$$