Can You Bob and Weave?

Fiddler

From Andrew E. Love comes a puzzle that’s sure to hook your attention:

A weaving loom set comes with a square with equally spaced hooks along each of its sides, as well as elastic bands that can be attached to the hooks.

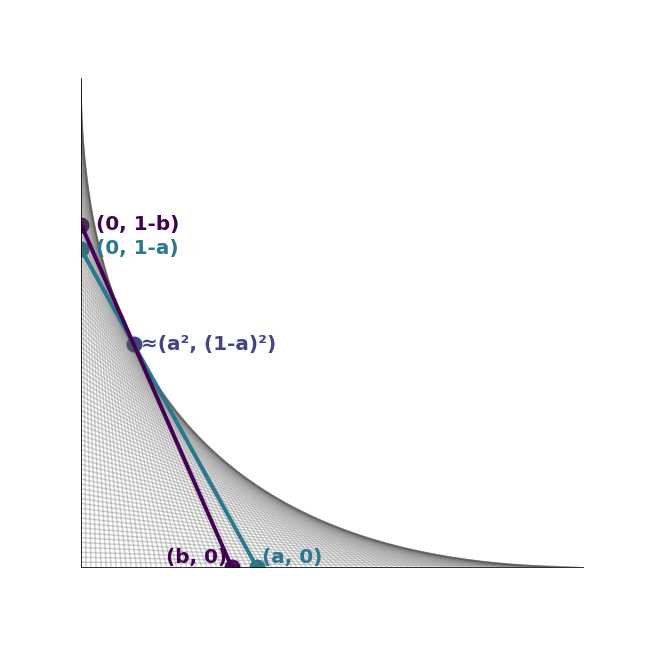
Suppose a particular weaving loom has N hooks on each side, evenly spaced from one corner to another (i.e., there are two hooks on the two corners and N−2 hooks between them). Let’s label the hooks along one side A₁ through A_N, the hooks on the next clockwise side B₁ through B_N (with A_N and B₁ denoting the same hook), the hooks on the third clockwise side C₁ through C_N, and the hooks on the final side D₁ through D_N.

Next, let’s use a whole bunch of elastic bands to connect hooks A₁ and B₁, A₂ and B₂, A₃ and B₃, and so on, up to A_N and B_N. When N is 100, here’s what the loom looks like:

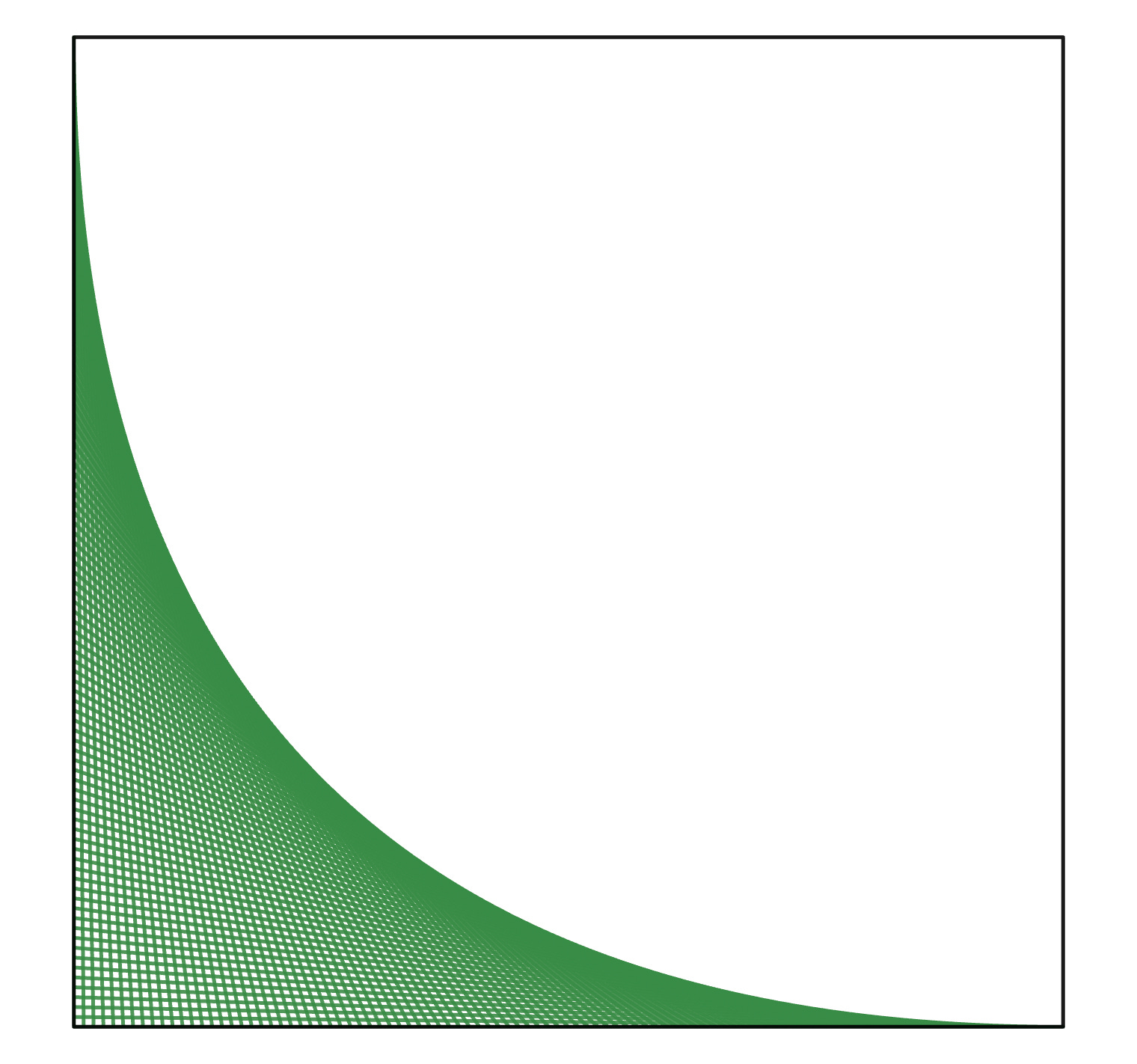
As N increases, what is the shape of the curve formed by the edges of the bands? Your answer can be a single word or a mathematical equation.

Solution

Consider the N hooks are spaced from $0$ to $1$. The line connecting points $(a,0)$ and $(0,1-a)$ has slope $m = \dfrac{a-1}{a}$ and equation

$$y = \left(\dfrac{a-1}{a}\right)x + -(a-1)$$
This can be expressed as:

$$ay = (x-a)(a-1)$$
Similary, the line connecting points $(b,0)$ and $(0,1-b)$ has slope $m = \dfrac{b-1}{b}$ and the equation can be expressed as:

$$by = (x-b)(b-1)$$
Multiply by $b$ and $-a$ and adding yields

$$0 = b(x-a)(a-1)-a(x-b)(b-1)$$
$$0 = -a^2b + abx + ab - bx - abx + ab^2 - ab + ax$$
$$-ax + bx = -a^2b + ab^2$$
$$x = ab$$.
$$\lim_{b\to a} x = a^2$$
Substituting:

$$ay = (a^2-a)(a-1)$$
$$y = (1-a)^2$$

Since, every point on the formed curve has coordinates $\left(a^2, (1-a)^2\right)$ and slope $m = \dfrac{a-1}{a}$, the derivative of the curve can be represented as:

$$\dfrac{dy}{dx} = \dfrac{-\sqrt{y}}{\sqrt{x}}$$
$$\dfrac{dy}{\sqrt{y}} = \dfrac{-dx}{\sqrt{x}}$$
$$\int \dfrac{dy}{\sqrt{y}} = -\int \dfrac{-dx}{\sqrt{x}}$$
$$ 2\sqrt{y}= -2\sqrt{x} + C$$
Given points $(0,1)$ and $(1,0)$,

$$\sqrt{y}= 1 - \sqrt{x}$$
Squaring both sides yields:

$$y = x + 1 - 2\sqrt{x}$$
$$x^2 + y^2 - 2xy + 2x - 2y + 1 = 4x$$
$$x^2 - 2xy + y^2 - 2x - 2y + 1 = 0$$

Answer

Looking at the discriminant, $B^2-4AC = (-2)^2 -4(1)(1) = 0$.

Thus, the formed curve is a part of a parabola.

Rohan Lewis

2023.09.11

Code can be found here.