Can You Bob and Weave All the Way Around?

Fiddler

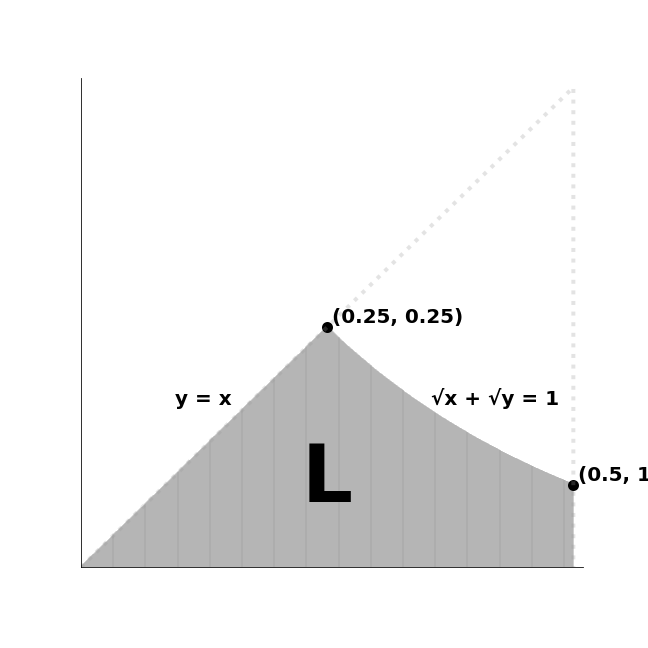
Let’s quadruple the number of bands placed on the weaving loom. In addition to the band connecting A₁ and B₁, you also place bands connecting B₁ and C₁, C₁ and D₁, and D₁ and A₁. You do this for all the sets of hooks from 1 through N, so that a total of 4N bands have been placed.

When N is 100, here is what the loom looks like:

As N increases, what fraction of the loom’s area lies between the four sets of bands? In other words, what fraction of the square above does the central white region make up?

Solution

Note that the problem can be solved by determining the value of $1-8L$

$$L =\int\limits_0^{1/4} xdx +\int\limits_{1/4}^{1/2} (1-\sqrt{x})^2dx$$

$$=\int\limits_0^{1/4} xdx +\int\limits_{1/4}^{1/2} (x - 2\sqrt{x} +1)dx$$
$$=\dfrac{x^2}{2} \Biggr]_0^{1/2} + \left(- \dfrac{4x^{3/2}}{3} + x\right)\Biggr]_{1/4}^{1/2}$$
$$=\left(\dfrac{1}{8} - 0\right) + \left(\left(-\dfrac{\sqrt{2}}{3} + \dfrac{1}{2}\right) - \left(-\dfrac{1}{6}+ \dfrac{1}{4}\right)\right)$$ $$=\dfrac{13}{24} - \dfrac{\sqrt{2}}{3}$$
Solving for the entire figure:

$$A = 1 - 8 \left(\dfrac{13}{24} - \dfrac{\sqrt{2}}{3}\right)$$
$$1 - \dfrac{13}{3} + \dfrac{8\sqrt{2}}{3}$$

Answer

$$\dfrac{8\sqrt{2}}{3} - \dfrac{10}{3} \approx 0.4379$$

Rohan Lewis

2023.09.11

Code can be found here.