Can You Make Something out of Nothing?

Fiddler

From Jeremy Dixon comes a tale of two functions:

Consider f(n) = 2n+1 and g(n) = 4n. It’s possible to produce different whole numbers by applying combinations of f and g to 0. For example, f(0) = 1, f(f(0)) = 3, g(f(0)) = 4, f(f(f(0))) = 7, f(g(f(0))) = 9, f(f(f(f(0)))) = 15, and g(g(f(0))) = 16.

How many whole numbers between 1 and 1,024 (including 1 and 1,024) can you produce by applying some combination of f’s and g’s to the number 0?

Solution

Compositions:

I will first look at the total number.

Composition of 0 functions.

$n = 0$. There is one number in the set.

Composition of 1 function.

$f(n) = 1$ and $g(n) = 0$. There are two numbers in the set, and 1 is new.

Composition of 2 functions.

$f(f(n)) = 3$ and $g(f(n)) = 4$. Note that $f(g(n)) = 1$ and $g(g(n)) = 0$. There are four numbers in the set, and two are new.

...

Composition of k functions.

There are $2^k$ numbers in the set, and $2^{k-1}$ are new.

What is k?:

$2^{10} = 1024$ and $g^5(f(0)) = 4^5\cdot(1) = 1024$.

Because $f$ approximately doubles numbers, and $g$ quadruples numbers, the maximum number of compositions necessary to yield all feasible numbers $0 \le n \le 1024$ is ten.

$f^{10}(0) = 512 + 256 + \cdots + 2 + 1 = 1023$ is the only new number added at the 10^th composition.

$2^{10} = 1024$. However, many of those $1024$ numbers in the set of values from combinations of ten compositions are greater than $1024$...

Answer

I ran code and achieved the following results.

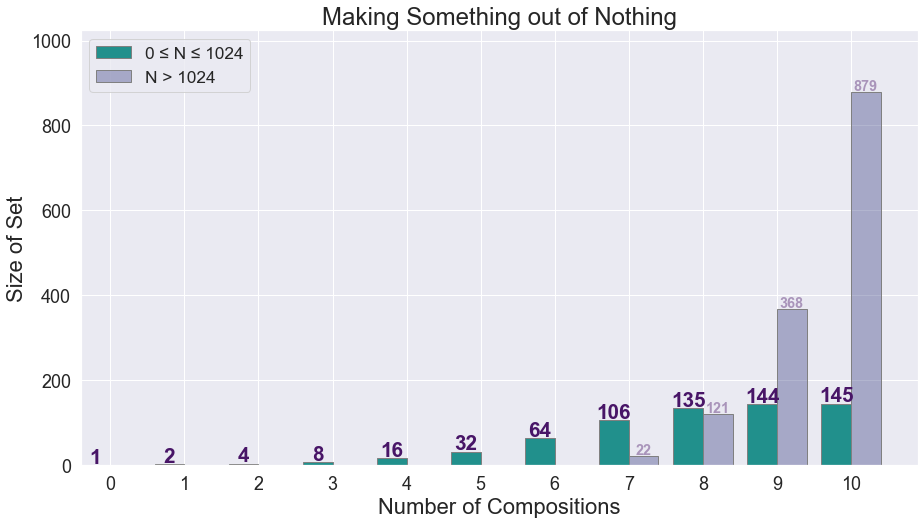
$145$ numbers between $0$ to $1024$ can be produced from combinations of $f$ and $g$.

Those numbers are :

$1, 3, 4, 9, 11, 12, 15, 16, 33, 35, 36, 41, 43, 44, 47, 48, 57, 59, 60, 63, 64, 129, 131, 132, 137, 139, 140, 143, 144, 161,$ $163, 164, 169, 171, 172, 175, 176, 185, 187, 188, 191, 192, 225, 227, 228, 233, 235, 236, 239, 240, 249, 251, 252, 255, $ $256, 513, 515, 516, 521, 523, 524, 527, 528, 545, 547, 548, 553, 555, 556, 559, 560, 569, 571, 572, 575, 576, 641, 643, $ $644, 649, 651, 652, 655, 656, 673, 675, 676, 681, 683, 684, 687, 688, 697, 699, 700, 703, 704, 737, 739, 740, 745, 747, $ $748, 751, 752, 761, 763, 764, 767, 768, 897, 899, 900, 905, 907, 908, 911, 912, 929, 931, 932, 937, 939, 940, 943, 944, $ $953, 955, 956, 959, 960, 993, 995, 996, 1001, 1003, 1004, 1007, 1008, 1017, 1019, 1020, 1023, 1024$

Rohan Lewis

2023.07.30

Code can be found here.