Can You Make Something and Negative Something out of Nothing?

Extra Credit

Now consider the functions g(n) = 4n and h(n) = 1−2n. How many integers between -1,024 and 1,024 (including -1,024 and 1,024) can you produce by applying some combination of g’s and h’s to the number 0?

Solution

Compositions:

I will first look at the total number.

Composition of 0 functions.

$n = 0$. There is one number in the set.

Composition of 1 function.

$g(n) = 0$ and $h(n) = 1$. There are two numbers in the set, and 1 is new.

Composition of 2 functions.

$g(h(n)) = 4$ and $h(h(n)) = -1$. Note that $g(g(n)) = 0$ and $h(g(n)) = 1$. There are four numbers in the set, and two are new.

...

Composition of k functions.

There are $2^k$ numbers in the set, and $2^{k-1}$ are new.

What is k?:

$2^{10} = 1024$ and $h^5(g(0)) = 4^5\cdot(1) = 1024$.

Because $h$ negates and approximately doubles numbers, and $g$ quadruples numbers, the maximum number of compositions necessary to yield all feasible numbers $-1024 \le n \le 1024$ is eleven.

$h^{11}(0) = 1 - 2 + 4 - ... - 512 + 1024 = 683$ is the only new number added at the 11^th composition.

$2^{11} = 2048$. However, many of those $2048$ numbers in the set of values from combinations of eleven compositions are less than $-1024$ or greater than $1024$...

Answer

I ran code and achieved the following results.

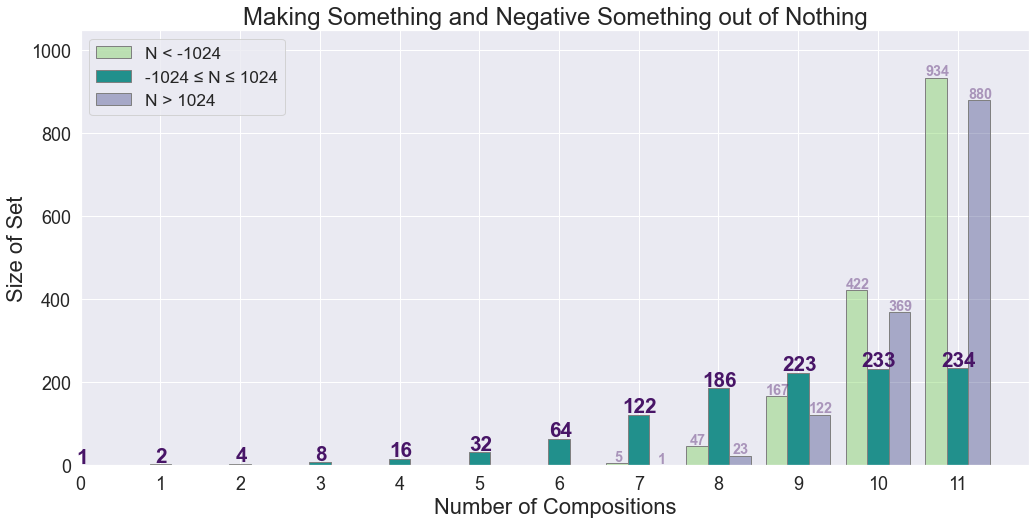
$234$ numbers between $-1024$ to $1024$ can be produced from combinations of $g$ and $h$.

Those numbers are :

$-1024, -511, -509, -508, -503, -501, -500, -497, -496, -479, -477, -476, -471, -469, -468, -465, -464, -455, -453, -452, -449,$ $-448, -383, -381, -380, -375, -373, -372, -369, -368, -351, -349, -348, -343, -341, -340, -337, -336, -327, -325, -324, -321,$ $-320, -287, -285, -284, -279, -277, -276, -273, -272, -263, -261, -260, -257, -256, -127, -125, -124, -119, -117, -116, -113,$ $-112, -95, -93, -92, -87, -85, -84, -81, -80, -71, -69, -68, -65, -64, -31, -29, -28, -23, -21, -20, -17, -16, -7, -5, -4, -1, 0,$ $1, 3, 4, 9, 11, 12, 15, 16, 33, 35, 36, 41, 43, 44, 47, 48, 57, 59, 60, 63, 64, 129, 131, 132, 137, 139, 140, 143, 144, 161, 163, 164, 169, 171, 172,$ $175, 176, 185, 187, 188, 191, 192, 225, 227, 228, 233, 235, 236, 239, 240, 249, 251, 252, 255, 256, 513, 515, 516, 521, 523, 524, 527, 528,$ $545, 547, 548, 553, 555, 556, 559, 560, 569, 571, 572, 575, 576, 641, 643, 644, 649, 651, 652, 655, 656, 673, 675, 676, 681, 683, 684, 687,$ $688, 697, 699, 700, 703, 704, 737, 739, 740, 745, 747, 748, 751, 752, 761, 763, 764, 767, 768, 897, 899, 900, 905, 907, 908, 911, 912, 929,$ $931, 932, 937, 939, 940, 943, 944, 953, 955, 956, 959, 960, 993, 995, 996, 1001, 1003, 1004, 1007, 1008, 1017, 1019, 1020, 1023, 1024$

Rohan Lewis

2023.07.30

Code can be found here.